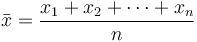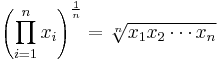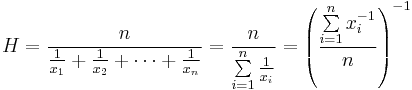Mittelwert vs. Median

- 3347
- 341
- Kurt Reinelt
Bedeuten (oder durchschnittlich) und Median sind statistische Begriffe, die eine ähnliche Rolle im Hinblick auf das Verständnis des Verständnisses spielen zentrale Tendenz einer Reihe statistischer Punkte. Während ein Durchschnitt traditionell ein beliebtes Maß für einen Mittelpunkt in einer Stichprobe war, hat er den Nachteil, dass ein einzelner Wert im Vergleich zum Rest der Stichprobe zu hoch oder zu niedrig ist. Deshalb wird ein Median manchmal als besseres Maß für einen mittleren Punkt angenommen.
Vergleichstabelle
| Bedeuten | Median | |
|---|---|---|
| Definition | Der Mittelwert ist der arithmetische Durchschnitt einer Reihe von Zahlen oder Verteilung. Es ist das am häufigsten verwendete Maß für die zentrale Tendenz einer Reihe von Zahlen. | Der Median wird als numerischer Wert beschrieben, der die höhere Hälfte einer Probe, eine Population oder eine Wahrscheinlichkeitsverteilung von der unteren Hälfte trennt. |
| Anwendbarkeit | Der Mittelwert wird für Normalverteilungen verwendet. | Der Median wird im Allgemeinen für verzerrte Verteilungen verwendet. |
| Relevanz für den Datensatz | Der Mittelwert ist kein robustes Werkzeug, da es weitgehend von Ausreißern beeinflusst wird. | Der Median eignet sich besser für verzerrte Verteilungen, um bei zentraler Tendenz abzuleiten, da er viel robuster und vernünftiger ist. |
| Wie man rechnet | Ein Mittelwert wird berechnet, indem alle Werte addiert und diese Bewertung durch die Anzahl der Werte geteilt werden. | Der Median ist die Zahl in der genauen Mitte des Wertesatzes. Ein Median kann berechnet werden, indem alle Zahlen in aufsteigender Reihenfolge aufgelistet und dann die Nummer in der Mitte dieser Verteilung gefunden werden. |
Definitionen von Mean und Median
In Mathematik und Statistik der Mittelwert oder der arithmetisches Mittel einer Liste von Zahlen ist die Summe der gesamten Liste geteilt durch die Anzahl der Elemente in der Liste. Bei der Betrachtung symmetrischer Verteilungen ist der Mittelwert wahrscheinlich die beste Maßnahme, um die zentrale Tendenz zu erreichen. In Wahrscheinlichkeitstheorie und Statistik a Median Ist diese Zahl, die die höhere Hälfte einer Stichprobe, einer Population oder einer Wahrscheinlichkeitsverteilung von der unteren Hälfte trennt?.
Wie man rechnet
Der Bedeuten oder der Durchschnitt ist wahrscheinlich die am häufigsten verwendete Methode zur Beschreibung der zentralen Tendenz. Ein Mittelwert wird berechnet, indem alle Werte addiert und diese Bewertung durch die Anzahl der Werte geteilt werden. Der arithmetisches Mittel einer Probe  Ist die Summe die abgetasteten Werte geteilt durch die Anzahl der Elemente in der Stichprobe:
Ist die Summe die abgetasteten Werte geteilt durch die Anzahl der Elemente in der Stichprobe:
Der Median ist die Zahl in der genauen Mitte des Wertesatzes gefunden. Ein Median kann berechnet werden, indem alle Zahlen in aufsteigender Reihenfolge aufgelistet und dann die Nummer in der Mitte dieser Verteilung gefunden werden. Dies gilt für eine ungerade Zahlenliste. Bei einer geraden Anzahl von Beobachtungen gibt es keinen einzigen mittleren Wert, daher ist es eine übliche Praxis, den Mittelwert der beiden mittleren Werte zu nutzen.
Beispiel
Nehmen wir an, dass es in einer Klasse neun Schüler mit den folgenden Punktzahlen in einem Test gibt: 2, 4, 5, 7, 8, 10, 12, 13, 83. In diesem Fall die durchschnittliche Punktzahl (oder die bedeuten) ist die Summe aller Punkte geteilt durch neun. Dies entspricht 144/9 = 16. Beachten Sie, dass 16, obwohl 16 der arithmetische Durchschnitt ist, durch den ungewöhnlich hohen Score von 83 im Vergleich zu anderen Bewertungen verzerrt wird. Fast alle Ergebnisse der Schüler sind unter der Durchschnitt. In diesem Fall ist der Mittelwert daher kein guter Vertreter der zentrale Tendenz dieser Stichprobe.
Der Median, Auf der anderen Seite ist der Wert, der so ist. In diesem Beispiel ist der Median 8. Es gibt vier Punkte unten und vier über dem Wert 8. Also repräsentiert 8 den mittleren Punkt oder die zentrale Tendenz der Probe.
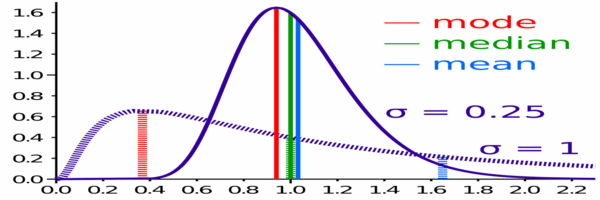 Vergleich von Mittelwert, Median und Modus von zwei logarithmischen Normalverteilungen mit unterschiedlicher Schiefe.
Vergleich von Mittelwert, Median und Modus von zwei logarithmischen Normalverteilungen mit unterschiedlicher Schiefe. Nachteile von arithmetischen Mitteln und Medianen
Der Mittelwert ist kein robustes statistisches Instrument, da es nicht auf alle Verteilungen angewendet werden kann, aber mit Sicherheit das am weitesten verbreitete statistische Instrument ist, um die zentrale Tendenz abzuleiten. Der Grund, warum der Mittelwert nicht auf alle Verteilungen angewendet werden kann.
Der Nachteil des Median ist, dass es schwierig ist, theoretisch umzugehen. Es gibt keine einfache mathematische Formel, um den Median zu berechnen.
Andere Arten von Mitteln
Es gibt viele Möglichkeiten, die zentrale Tendenz oder den Durchschnitt einer Reihe von Werten zu bestimmen. Der oben diskutierte Mittelwert ist technisch gesehen der arithmetische Mittelwert und die am häufigsten verwendete Statistik für den Durchschnitt. Es gibt andere Arten von Mitteln:
Geometrisches Mittelwert
Der geometrische Mittel ist definiert als der Ndie Wurzel des Produkts von N Zahlen, ich.e., für eine Reihe von Zahlen X1,X2,… ,XN, Der geometrische Mittel ist definiert als
Geometrische Mittel sind besser als arithmetische Mittel zur Beschreibung eines proportionalen Wachstums. Eine gute Anwendung für den geometrischen Mittelwert ist beispielsweise die Berechnung der zusammengesetzten jährlichen Wachstumsrate (CAGR).
Harmonische Mittel
Der harmonische Mittelwert ist der Gegenstand des arithmetischen Mittelwerts des Reziprocals. Das harmonische Mittel H der positiven realen Zahlen X1,X2,… ,XN Ist
Eine gute Anwendung für harmonische Mittel besteht darin. Für Exampe ist es besser, bei der Berechnung des durchschnittlichen Preisverhältnisses (P/E) gewichteten harmonischen Mittelwert zu verwenden, um das durchschnittliche Preis-Leistungs-Verhältnis zu berechnen. Wenn die P/E -Verhältnisse unter Verwendung eines gewichteten arithmetischen Mittelwerts gemittelt werden, erhalten hohe Datenpunkte übermäßig höhere Gewichte als niedrige Datenpunkte.
Pythagoräische Mittel
Der arithmetische Mittelwert, der geometrische Mittelwert und der harmonische Mittel zusammen bilden zusammen eine Reihe von Mitteln, die als pythagoräische Mittel bezeichnet werden. Für jede Reihe von Zahlen ist der harmonische Mittelwert immer das kleinste aller pythagoräischen Mittel, und das arithmetische Mittel ist immer das größte der 3 Mittelwerte. ich.e. Harmonischer Mittelwert ≤ geometrisches Mittelwert ≤ arithmetisches Mittelwert.
Andere Bedeutungen der Wörter
Bedeuten kann als Sprachfigur verwendet werden und enthält eine literarische Referenz. Es wird auch verwendet, um arm zu implizieren oder nicht großartig zu sein. Median, In einer geometrischen Referenz befindet sich eine gerade Linie, die von einem Punkt im Dreieck zur Mitte der gegenüberliegenden Seite verläuft.