Unterschied zwischen Bereich und Oberfläche

Fläche gegen Oberfläche

Die Mathematik hat Möglichkeiten, uns zum Nachdenken zu bringen und zu überdenken und es noch einmal zu tun. Als ob die Mathematik nicht verwirrend genug wäre und durch ihre Formeln, Operationen und Ableitungen hervorgerufen worden wäre - können Menschen auch mit Definitionen verwechselt werden, insbesondere mit ähnlichen Begriffen.

Die meisten von uns wissen, dass Geometrie die Mathematik der Messung von Erde, Räumen, Form und Figuren ist.

Fläche ist häufig ein Ausdruck der Größe einer 2-dimensionalen Ebene. Es wird in vielen verschiedenen Einheiten ausgedrückt. Diese Einheiten umfassen: Quadratmeter, Hektar, Quadratkilometer, Quadratmeter, Quadratmeter, quadratische Sicht, Hektar und quadratische Meile, um nur einige zu nennen.

Eine der grundlegendsten bekannten Flächenformeln ist die eines Rechtecks, das mit der Breite (L x W) multipliziert wird, und im Fall des Quadrats ist es eine Länge eines Seitenquadrats (Sâ²).

Andere Formeln sind:

Dreieck '„½ bh; Wo B ist Basis und H ist Größe.

Rhombus '„½ AB; wo a und b Längen der beiden Diagonalen sind.

Parallelogramm "BH; wobei B die Grundlänge ist und H die senkrechte Höhe ist.

Trapez '„½ (a + b) h; wobei a und b die Länge der parallelen Seiten sind und H die Höhe ist.

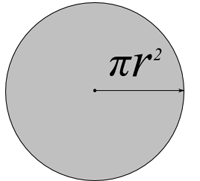
Kreis '“prâ²; wobei R die Länge des Radius ist (das Quadrat der Radiuszeit pi).

Der Bereich wird oft mit "Oberfläche" verwechselt, was technisch gesehen gleich ist, wenn er in zweidimensionalen Oberflächen entspricht. Es wird jedoch angemessener verwendet, um die Größe einer exponierten Oberfläche durch einen bestimmten Feststoff auszudrücken, der dreidimensional ist. Zum Beispiel hat ein Würfel eine Oberfläche, die der Summe der Flächen aller sechs Seiten (6sâ²) entspricht.

Wie die Fläche wird auch die Oberfläche in quadratischen Einheiten ausgedrückt.

Formeln von Oberflächen einiger Festkörper:

Zylinder - 2Prâ² (R + H); Wo R Radius ist und H die Höhe des Zylinders ist.

Kegel - pr (r + l); Wo R der Radius ist und L die schräge Höhe des Kegels ist.

Sphere '“4Prâ²; Wo R der Radius ist.

Zusammenfassung:

1. Der Begriff Bereich ist ein allgemeiner Begriff, der die Größenmessung einer Oberfläche ausdrückt, während die Oberfläche eher angemessen verwendet wird, um die Messung der freiliegenden Oberfläche eines bestimmten festen Objekts auszudrücken.

2. Die Fläche ist für zweidimensionale flache Oberflächen, während die Oberfläche für dreidimensionale Feststoffe gilt.