Allgemein

Unterschied zwischen T-Test und ANOVA

Unterschied zwischen T-Test und ANOVA

Es gibt eine dünne Linie von Abgrenzung inmitten von T-Test und Anova, ich.e. Wenn das Bevölkerungsmittelmittel von nur zwei Gruppen verglichen werden soll, die T-Test wird verwendet, aber wenn Mittel von mehr als zwei Gruppen verglichen werden sollen, Anova Ist bevorzugt.

T-Test und Analyse der als ANOVA abgekürzten Varianz sind zwei parametrische statistische Techniken, die zur Prüfung der Hypothese verwendet werden. Da diese auf der gemeinsamen Annahme basieren, wie die Population, aus der die Stichprobe stammt zwei.

Hier ist ein Artikel, in dem Sie den signifikanten Unterschied zwischen T-Test und ANOVA verstehen, einen Blick darauf werfen.

Inhalt: T-Test gegen Anova

  1. Vergleichstabelle
  2. Definition
  3. Schlüsselunterschiede
  4. Abschluss

Vergleichstabelle

VergleichsgrundlageT-TestAnova
BedeutungT-Test ist ein Hypothesentest, mit dem die Mittelwerte von zwei Populationen verglichen werden.ANOVA ist eine statistische Technik, mit der die Mittel von mehr als zwei Populationen verglichen werden.
Teststatistik(x ̄-µ)/(s/√n)Zwischen Stichprobenvarianz/innerhalb der Stichprobenvarianz

Definition des T-Tests

Der T-Test wird als statistischer Test beschrieben, bei dem untersucht. Es ist ein Instrument zur Analyse, ob die beiden Proben aus derselben Population stammen.

Der Test basiert auf t-Statistik, was davon ausgeht.

In T-Test nimmt die Hypothese von H die Form von H0: µ (x) = µ (y) gegen die alternative Hypothese h1: µ (x) ≠ µ (y), wobei µ (x) und µ (y) die Populationsmittelwerte darstellen. Der Grad der Freiheit des T-Tests ist n1 + N2 - 2

Definition von ANOVA

Die Varianzanalyse (ANOVA) ist eine statistische Methode, die häufig in all jenen Situationen verwendet wird, in denen ein Vergleich zwischen mehr als zwei Bevölkerungswerten wie der Ernteausbeute aus mehreren Samensorten durchgeführt werden soll. Es ist ein wesentliches Analysewerkzeug für den Forscher, mit dem er gleichzeitig Tests durchführen kann. Wenn wir ANOVA verwenden, wird angenommen, dass die Stichprobe aus der normal verteilten Bevölkerung stammt und die Bevölkerungsvarianz gleich ist.

In ANOVA ist die Gesamtvariation in einem Datensatz in zwei Typen aufgeteilt, i, i.e. Die Menge, die für Zufall und Betrag zugewiesen wurde, die bestimmten Ursachen zugewiesen sind. Sein Grundprinzip besteht darin, die Varianzen zwischen den Bevölkerungsmitteln zu testen, indem die Variationsmenge innerhalb der Gruppenelemente bewertet wird, proportional zu der Menge der Variation zwischen den Gruppen. Innerhalb der Probe liegt die Varianz auf die zufällige ungeklärte Störung, während eine unterschiedliche Behandlung zwischen der Probenvarianz verursachen kann.

Mit der Verwendung dieser Technik testen wir Nullhypothese (H. H0) wobei alle Bevölkerungswerte gleich sind oder alternative Hypothese (H)1) wobei mindestens eine Bevölkerung unterschiedlich ist.

Schlüsselunterschiede zwischen T-Test und ANOVA

Die signifikanten Unterschiede zwischen T-Test und ANOVA werden in den folgenden Punkten ausführlich erörtert:

  1. Ein Hypothesentest, der zum Vergleich der Mittel von zwei Populationen verwendet wird, wird als T-Test bezeichnet. Eine statistische Technik, mit der die Mittelwerte von mehr als zwei Populationen verglichen werden, wird als Varianzanalyse oder ANOVA bezeichnet.
  2. Die Teststatistik für T-Test ist: 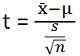  Die Teststatistik für ANOVA ist: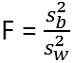

Abschluss

Nach der Überprüfung der oben genannten Punkte kann gesagt werden. Obwohl die Wahrscheinlichkeit von Fehlern zunehmen könnte, wenn T-Test verwendet wird, wenn wir mehr als zwei Mittel der Populationen gleichzeitig vergleichen müssen, wird ANOVA verwendet