Unterschied zwischen horizontaler und vertikaler Asymptote

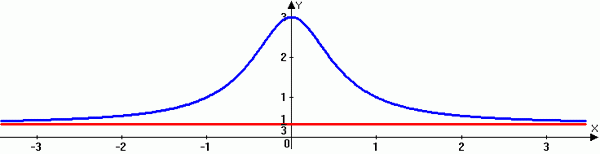
Bevor wir uns mit dem Thema horizontaler und vertikaler Asymptote einlassen, versuchen wir zu verstehen, was genau Asymptoten sind und welche Rolle sie in der Mathematik spielen. In der projektiven Geometrie ist eine Asymptote eine geraden Linie, die sich einer bestimmten Kurve willkürlich nähert, sich jedoch nicht in irgendeiner endlicher Entfernung trifft. Geometrisch ist eine Linie eine Asymptote einer Kurve y = f (x), wenn der Abstand zwischen der Linie und einem Punkt 'P' auf der Kurve Null nähert. Ein Diagramm kann eine Asymptote parallel zu jeder Achse haben. Tatsächlich ist eine Asymptote etwas, das nicht physisch da ist - es ist eher wie das Glauben.

Eine Asymptote hilft dabei. Es ist einfach eine imaginäre Linie, die Ihnen hilft, eine rationale Funktion zu gratschen. Wenn sich die Kurve zu einer Asymptote nähert, kommt sie der Asymptote immer näher und berührt sie nie wirklich. Somit hilft die Asymptote, zu bestimmen, wo der Diagramm der Funktion gehen kann oder nicht gehen kann oder nicht. Davon abgesehen gibt es drei Arten von Asymptoten: vertikale, horizontale und schräge Asymptoten. Aber wir werden nur vertikale Asymptoten und horizontale Asymptoten diskutieren und sehen, wie man herausfindet, was eigentlich was ist.

Was ist horizontale Asymptote?

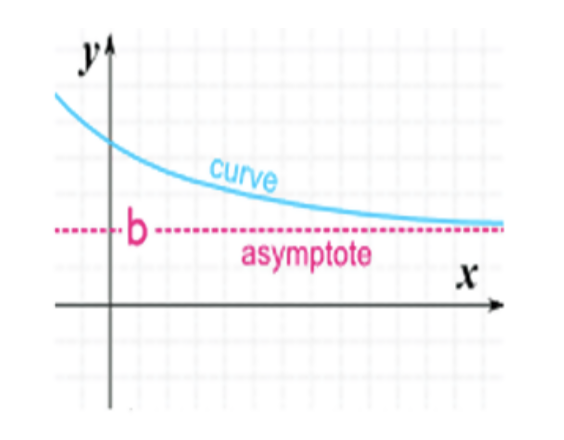
Eine horizontale Asymptote ist ein konstanter Wert in einem Diagramm, das sich einer Funktion nähert, aber tatsächlich nicht erreicht. Es zeigt an, was tatsächlich mit der Kurve passiert, wenn die X-Werte sehr groß oder sehr klein werden. In den obigen grafischen Beispielen nähert sich die Kurve einem konstanten Wert B, aber nie erreicht y = 0.

Die Linie y = b ist eine horizontale Asymptote des Diagramms von 'f' Wenn f (x) -> B als x -> ∞ oder x -> -∞

Um eine horizontale Asymptote einer rationalen Funktion zu finden, ist der Grad der Polynome im Zähler und des Nenners zu berücksichtigen.

• Wenn der Nenner in der Funktionsgleichung die höchste variable Leistung aufweist, ist die horizontale Asymptote automatisch die x-Achse oder y = 0.
• Wenn sowohl der Zähler als auch der Nenner einen gleichen Grad haben, nehmen Sie die führenden Koeffizienten dieser Begriffe mit der höchsten Leistung ein und machen
• Wenn der Zähler in der Funktionsgleichung die höchste variable Leistung aufweist, hat die Funktion keine horizontale Asymptote; Die Grafik wird wahrscheinlich eine schräge Asymptote haben.

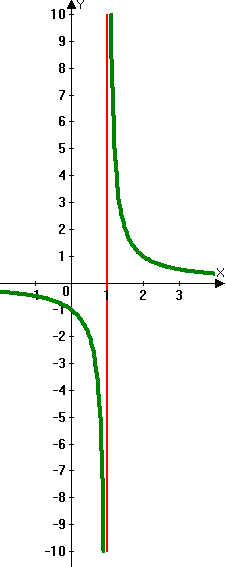
Was ist vertikale Asymptote?

Da der Nenner eines Bruchs niemals Null sein kann, kann die Variable unten ein Problem sein, wenn ein Bruchteil ein Problem sein kann. Ein gewisser Domänenwert von 'x' macht den Nenner Null und die Funktion springt über diesen Wert in der Grafik, wodurch eine vertikale Asymptote erstellt wird. Sie sind vertikale Linien, die leicht oder mit Strichen gezeichnet sind, um zu zeigen, dass sie nicht Teil des Diagramms sind.

Wenn die reelle Zahl 'a' eine Null des Nenner q (x) ist, dann haben der Diagramm von f (x) = p (x)/q (x), wobei P (x) und q (x) kein gemeinsames haben Faktoren hat die vertikale Asymptote x = a.

Unterschied zwischen horizontaler und vertikaler Asymptote

Definition

- Eine horizontale Asymptote ist ein konstanter Wert in einem Diagramm, das sich einer Funktion nähert, aber tatsächlich nicht erreicht. Es zeigt an, was tatsächlich mit der Kurve passiert, wenn die X-Werte sehr groß oder sehr klein werden. Vertikale Asymptoten hingegen sind unsichtbare vertikale Linien, die der Null im Nenner einer rationalen Fraktion entsprechen. Sie sind vertikale Linien, die leicht oder mit Strichen gezeichnet sind, um zu zeigen, dass sie nicht Teil des Diagramms sind.

Berechnung

- Um eine horizontale Asymptote einer rationalen Funktion zu bestimmen, ist der Grad der Polynome im Zähler und des Nenners zu berücksichtigen. Wenn der Nenner in der Funktionsgleichung die höchste variable Leistung aufweist, ist die horizontale Asymptote automatisch die x-Achse oder y = 0. Wenn sowohl der Zähler als auch der Nenner einen gleichen Grad haben, machen Sie einen Bruchteil ihrer Koeffizienten, um die horizontale Asymptote -Gleichung zu bestimmen. Um die vertikalen Asymptoten einer rationalen Funktion zu bestimmen, setzen Sie den Nenner der Fraktion gleich Null.

Beispiel

- Lassen Sie uns die Asymptoten der Funktion herausfinden

Y = 3x²+9x-21 ∕ x²-25

Um die vertikalen Asymptoten zu finden, setzen Sie den Nenner der Fraktion gleich Null.

X²-25 = 0

(x-5) (x+5) = 0

x = 5 und x = - 5

Diese beiden Zahlen sind die beiden Werte, die nicht in der Domäne enthalten werden können, daher sind die Gleichungen vertikale Asymptoten. Die beiden vertikalen Asymptoten sind also x = 5 und x = - 5.

Um die horizontale Asymptote zu bestimmen, schauen Sie sich die ursprüngliche Gleichung an. Hier ist die höchste variable Leistung 2. Da sowohl der Zähler als auch der Nenner den gleichen Kraftgrad haben, machen Sie einen Bruchteil ihrer Koeffizienten:

y = 3x²/X²

y = 3/1

y = 3

Die Gleichung der horizontalen Asymptote ist also y = 3.

Horizontale Asymptote vs. Vertikale Asymptote: Vergleichstabelle

Zusammenfassung der horizontalen Asymptote vs. Vertikale Asymptote

Eine Asymptote hilft dabei. Vertikale Asymptoten markieren Orte, an denen die Funktion keine Domäne hat. Sie lösen die Gleichung der vertikalen Asymptoten, indem Sie den Nenner der Fraktion auf Null setzen. Horizontale Asymptoten dagegen geben an, was mit der Kurve passiert, wenn die X-Werte sehr groß oder sehr klein werden. Um eine horizontale Asymptote zu finden, müssen Sie den Grad der Polynome im Zähler und im Nenner berücksichtigen.