Unterschied zwischen Differenzierung und Integration

Kalkül ist eine der primären mathematischen Anwendungen, die heute in der Welt angewendet werden, um verschiedene Phänomen zu lösen. Es ist unter anderem in wissenschaftlichen Studien, Wirtschaftsstudien, Finanzen und Ingenieurwesen in hohem Maße beschäftigt, die eine wichtige Rolle im Leben eines Individuums spielen. Integration und Differenzierung sind die im Kalkül verwendeten Grundlagen, um Veränderungen zu untersuchen. Viele Menschen, einschließlich Studenten und Wissenschaftler, konnten jedoch nicht Unterschiede zwischen Differenzierung und Integration hervorheben.

Was ist Differenzierung?

Die Differenzierung ist ein Begriff, der im Kalkül verwendet wird, um sich auf die Änderung in der Eigenschaften zu beziehen, die sich in einer Änderung einer Einheit in einer anderen verwandten Eigenschaft befassen.

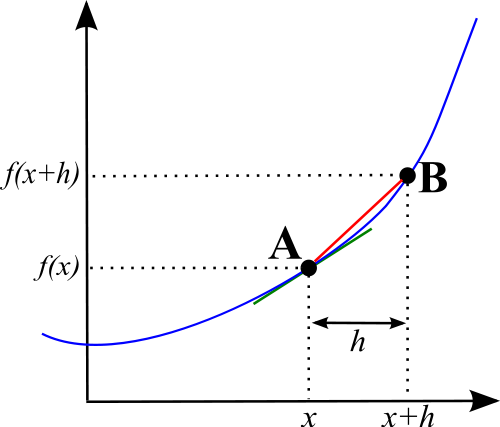
In einem anderen Begriff bildet die Differenzierung einen algebraischen Ausdruck, der bei der Berechnung des Gradienten einer Kurve an einem bestimmten Punkt hilft. Es ist wichtig hervorzuheben, dass Kurven ihre Hänge an einem bestimmten Punkt im Gegensatz zu geraden Linien variieren, die den gleichen Gradienten durchlaufen haben.

Was ist Integration?

Die Integration ist ein Begriff, der in Kalkül verwendet wird, um sich auf die Formel und das Verfahren zur Berechnung der Fläche unter der Kurve zu beziehen.

Es ist erwähnenswert, dass das Diagramm unter einer Kurve stehen muss, was zur Bildung eines integralen Teils führt, was schwierig ist, den Bereich im Gegensatz zu anderen Formen wie Kreisen, Quadraten und Rechtecken zu finden, die einfacher zu berechnen sind, um ihre Bereiche zu berechnen.

Unterschied zwischen Differenzierung und Integration

1) Zweck und Funktionen der Differenzierung und Integration

Integration und Differenzierung können hauptsächlich so differenziert werden, wie die beiden Konzepte angewendet werden und ihre ultimativen Ergebnisse. Sie werden verwendet, um zu unterschiedlichen Antworten zu gelangen, was der grundlegende Unterschied ist. Differenzierung wird zur Berechnung des Kurvegradienten verwendet. Nichtlineare Kurven haben an einem bestimmten Punkt unterschiedliche Hänge, was es schwierig macht, ihre Gradienten zu bestimmen. Die algebraische Expression zur Bestimmung der Änderung, die von einem Punkt zu einem anderen mit einer Einheit entstanden ist, wird als Differenzierung bezeichnet.  Andererseits ist die Integration ein algebraischer Ausdruck, der zur Berechnung der Fläche unter der Kurve verwendet wird, da sie keine perfekte Form ist, nachdem die Fläche leicht berechnet werden kann.

2) direkt gegenüber

Differenzierungs- und Integrations -Algebraikfunktionen sind direkt gegenüber einander entgegengesetzt, insbesondere in ihrer Anwendung. Wenn man eine Integration durchführt, soll er oder sie das Gegenteil von Differenzierung zeigen, während man Differenzierung durchführt, er oder sie entgegengesetzt von Integration durchführt. Zum Beispiel bilden Integrations- und Differenzierungsverhältnisse eine Beziehung, die ähnlich dargestellt wird, wenn man das Quadrat einer Zahl ausführt, und findet dann die Quadratwurzel des Ergebniss. Wenn man daher das Gegenteil einer integrierten Zahl finden möchte, muss er oder sie die Differenzierung derselben Zahl durchführen. Integration ist einfach der umgekehrte Differenzierungsprozess und umgekehrt.

3) Anwendung der realen Lebens für Differenzierung und Integration

In realen Szenarien wurde festgestellt. Dennoch ist es bemerkenswert zu hervorheben, dass beide Differenzierung essentielle Berechnungskonzepte sind, die das Leben einfach machen. Eine der Hauptanwendungen der Integration besteht darin.

Andererseits wird das Differenzierungskonzept bei der Berechnung der sofortigen Geschwindigkeit signifikant verwendet und zur Bestimmung verwendet, ob eine Funktion entsprechend zunimmt oder abnimmt. Dies ist eine klare Demonstration, wie die beiden Konzepte im Leben des Einzelnen angewendet werden.

4) Geschwindigkeit und Funktion der Differenzierung und Integration

Der andere Unterschied zwischen Integration und Differenzierung ist die Rolle, die sie spielen, wenn es um eine bestimmte untersuchte Funktion geht. Laut Mathematikern hilft die Differenzierung erheblich bei der Bestimmung der Funktionsgeschwindigkeit, indem sie bei der Berechnung der sofortigen Geschwindigkeit hilft. Auf der anderen Seite geht es dar. Es wird geschätzt, dass die Fläche unter der Kurve der von der Funktion zurückgelegten Strecke entspricht. Die algebraische Integrationsausdruck hilft bei der Berechnung der Fläche unter der Kurve, die die von der Funktion zurückgelegte Entfernung entspricht.

Algebraische Ausdrücke/Formel zur Differenzierung und Integration

Es ist auch erwähnenswert, dass Differenzierung und Integration unterschiedliche algebraische Ausdrücke aufweisen, die in der Berechnung verwendet werden. Dies erklärt, warum die beiden Kalkülkonzepte immer unterschiedliche Ergebnisse liefern werden.  Die Ableitung einer Funktion f (x) in Bezug auf die Variable x und gemäß der Produktregel wird definiert als:

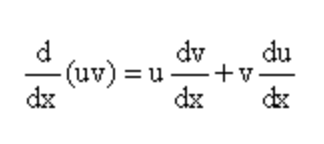
Andererseits kann die Integrationsformel oder die integrale Fläche unter der Kurve unter Verwendung der Formel berechnet werden:

∫f (x) dx, Welches ist die Formel, die unter Substitutionsmethode angewendet wurde.

5) Addition und Abteilung

Die andere Methode zum Vergleich der Integration mit der Differenzierung besteht darin, ausdrücklich zu erklären, wie jede Funktion ihre Ergebnisse realisiert. Die Integration bestimmt das Ergebnis einer spezifischen Funktion, indem die mit der Berechnung verbundenen Aspekte hinzugefügt werden. Andererseits bestimmt die Differenzierung die sofortige Geschwindigkeit und die Geschwindigkeit der Funktion durch Teilung.

Unterschiede zwischen Differenzierung und Integration: Vergleichstabelle

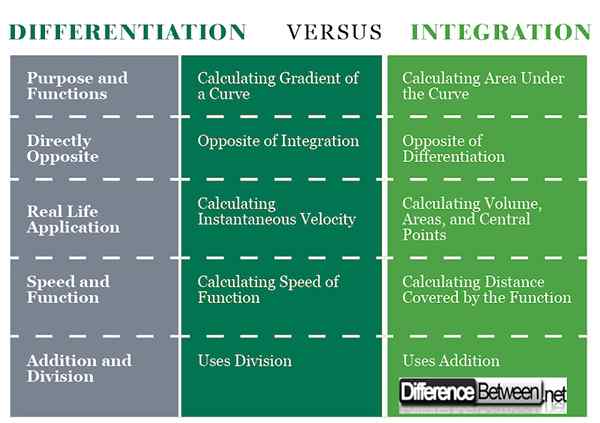
Zusammenfassung der Differenzierung vs. Integration

• Eine der Hauptschwankungen zwischen Differenzierung und Integration besteht darin, dass die beiden Kalkülfunktionen in ihrer Anwendung direkt voneinander entgegengesetzt sind.
• Schüler und andere Wissenschaftler sollten sich darauf konzentrieren, eines der Konzepte zu verstehen, nach denen sie das Gegenteil ausführen müssen, um die Ergebnisse der anderen Funktion zu bestimmen.
• Das Verständnis von Unterschieden zwischen Integration und Differenzierung ist wesentlich, da es den Einzelnen hilft, den richtigen algebraischen Ausdruck zu verwenden.
• Schließlich ist es von entscheidender Bedeutung, die beiden Kalkülkonzepte in der grundlegenden Mathematik zu beherrschen.