Unterschied zwischen bestimmten und unbestimmten Integralen
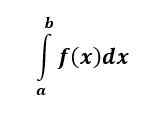
- 1918
- 64
- Prof. Dr. Dylan Hentschel
Kalkül ist ein wichtiger Zweig der Mathematik, und die Differenzierung spielt eine entscheidende Rolle im Kalkül. Der inverse Prozess der Differenzierung wird als Integration bezeichnet, und die Inverse wird als Integral oder einfach ausgedrückt bezeichnet, die Umkehrung der Differenzierung ergibt ein Integral. Basierend auf den Ergebnissen, die sie produzieren, werden die Integrale in zwei Klassen unterteilt, nämlich., definitive und unbestimmte Integrale.
Definitiv integral
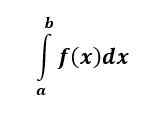
Das eindeutige Integral von f (x) ist eine Zahl und repräsentiert den Bereich unter der Kurve f (x) aus x = a Zu x = b.
Ein definitives Integral hat die oberen und unteren Grenzen für die Integrale und wird als definitiv bezeichnet, weil wir am Ende des Problems eine Zahl haben - es ist eine eindeutige Antwort.
Unbestimmtes Integral
Das unbestimmte Integral von F (x) ist eine Funktion und beantwortet die Frage: „Welche Funktion, wenn differenziert wird f (x)?”
Mit einem unbestimmten Integral gibt es hier keine oberen und unteren Grenzen des Integrals, und was wir erhalten, ist eine Antwort, die immer noch hat X's drin und wird auch eine Konstante haben (normalerweise bezeichnet durch C) drin.
Unbestimmte Integral liefert normalerweise eine allgemeine Lösung für die Differentialgleichung.
Unbestimmtes Integral ist eher eine allgemeine Form der Integration und kann als Anti-Derivat der betrachteten Funktion interpretiert werden.
Nehmen Sie an, die Funktionsdifferenzierung F führt zu einer anderen Funktion F, und die Integration von F gibt das Integral an. Symbolisch ist dies als geschrieben als
F (x) = ∫ƒ (x) dx
oder
F = ∫ƒ DX
wo beide F Und ƒ sind Funktionen von X, Und F ist differenzierbar. In der obigen Form wird es als Reimann -Integral bezeichnet und die resultierende Funktion begleitet eine willkürliche Konstante.
Ein unbestimmte Integral erzeugt häufig eine Funktionsfamilie; Daher ist das Integral unbestimmt.
Integrale und Integrationsprozess stehen im Mittelpunkt der Lösung von Differentialgleichungen. Im Gegensatz zu den Differenzierungsschritten folgen die Integrationsschritte jedoch nicht immer einer klaren und Standardroutine. Gelegentlich sehen wir, dass die Lösung nicht explizit in Bezug auf die Elementarfunktion ausgedrückt werden kann. In diesem Fall wird die analytische Lösung häufig in Form eines unbestimmten Integrals angegeben.
Grundsatz des Kalküls
Das Bestimmte und das unbestimmte Integral werden durch den grundlegenden Calculus -Theorem wie folgt verbunden: um a zu berechnen a definitiv integral, finde die unbestimmtes Integral (auch als Anti-Derivat bekannt) der Funktion und bewertet an den Endpunkten x = a Und x = b.
Der Unterschied zwischen bestimmten und unbestimmten Integralen wird erkennbar, sobald wir die Integrale für dieselbe Funktion bewertet haben.
Betrachten Sie das folgende Integral:
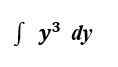
OK. Lassen Sie uns beide machen und den Unterschied sehen.
Zur Integration müssen wir dem Index einen hinzufügen, der uns zum folgenden Ausdruck führt:
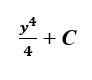
Zu diesem Zeitpunkt C ist nur eine Konstante für uns. In dem Problem sind zusätzliche Informationen erforderlich, um den genauen Wert von zu bestimmen C.
Lassen Sie uns das gleiche Integral in seiner definitiven Form i bewerten i.e., mit den oberen und unteren Grenzen enthalten.
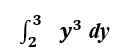
Grafisch gesehen berechnen wir jetzt den Bereich unter der Kurve f (x) = y3 zwischen y = 2 Und y = 3.
Der erste Schritt in dieser Bewertung ist der gleiche wie die unbestimmte Integral -Bewertung. Der einzige Unterschied besteht darin, dass wir diesmal die Konstante nicht hinzufügen C.
Der Ausdruck in diesem Fall sieht wie folgt aus:
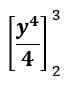
Dies führt zu:
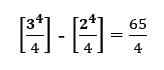
Im Wesentlichen haben wir 3 und dann 2 in den Ausdruck ersetzt und den Unterschied zwischen ihnen erhalten.
Dies ist der eindeutige Wert im Gegensatz zur Verwendung von Konstante C früher.
Erforschen wir den konstanten Faktor (in Bezug auf unbestimmte Integral) in einigen Details.
Wenn das Unterschied von y3 Ist 3y2, Dann
∫3y2dy = y3
Jedoch, 3y2 könnte das Unterschied vieler Ausdrücke sein, von denen einige enthalten y3-5, y3+7, usw… Dies impliziert, dass die Umkehrung nicht einzigartig ist, da die Konstante während der Operation nicht berücksichtigt wird.
Also im Allgemeinen, 3y2 ist das Unterschied von y3+C Wo C ist eine Konstante. Übrigens ist C als die bekannt "Konstante der Integration".
Wir schreiben das als:
∫ 3y2.dx = y3 + C
Integrationstechniken für ein unbestimmte Integral, wie z. Diese neuen Diskontinuitäten erscheinen, weil die Anti-Derivate die Einführung komplexer Logarithmen erfordern können.
Komplexe Logarithmen haben eine Sprungdiskontinuität, wenn das Argument die negative reale Achse überschreitet, und die Integrationsalgorithmen können manchmal keine Darstellung finden, in der diese Sprünge abbrechen.
Wenn das bestimmte Integral bewertet wird, indem zuerst ein unbestimmte Integral berechnet und dann die Integrationsgrenzen in das Ergebnis ersetzt werden, müssen wir uns bewusst sein, dass eine unbestimmte Integration möglicherweise Diskontinuitäten erzeugen kann. Wenn dies der Fall ist, müssen wir die Diskontinuitäten im Integrationsintervall untersuchen.

