Unterschied zwischen Korrelation und Regression
- 4595
- 593
- Milana Battke
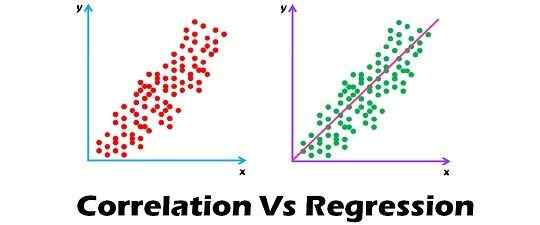
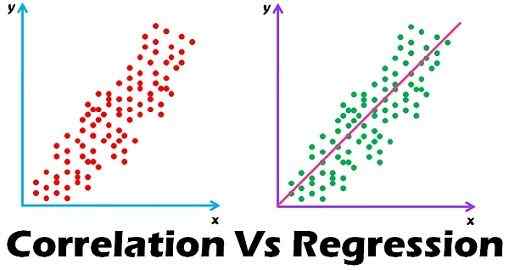 Korrelation und Regression sind die beiden Analysen, die auf einer multivariaten Verteilung basieren. Eine multivariate Verteilung wird als Verteilung mehrerer Variablen beschrieben. Korrelation wird als die Analyse beschrieben, die uns über die Assoziation oder das Fehlen der Beziehung zwischen zwei Variablen 'x' und 'y' informiert wird. Am anderen Ende, Regression Analyse sagt den Wert der abhängigen Variablen an, die auf dem bekannten Wert der unabhängigen Variablen basieren, unter der Annahme, dass die durchschnittliche mathematische Beziehung zwischen zwei oder mehr Variablen.
Korrelation und Regression sind die beiden Analysen, die auf einer multivariaten Verteilung basieren. Eine multivariate Verteilung wird als Verteilung mehrerer Variablen beschrieben. Korrelation wird als die Analyse beschrieben, die uns über die Assoziation oder das Fehlen der Beziehung zwischen zwei Variablen 'x' und 'y' informiert wird. Am anderen Ende, Regression Analyse sagt den Wert der abhängigen Variablen an, die auf dem bekannten Wert der unabhängigen Variablen basieren, unter der Annahme, dass die durchschnittliche mathematische Beziehung zwischen zwei oder mehr Variablen.
Der Unterschied zwischen Korrelation und Regression ist eine der häufig gestellten Fragen in Interviews. Darüber hinaus erleiden viele Menschen beim Verständnis dieser beiden Unklarheiten beim Verständnis dieser beiden. Lesen Sie diesen Artikel also vollständig, um diese beiden ein klares Verständnis zu haben.
Inhalt: Korrelation gegen Regression
- Vergleichstabelle
- Definition
- Schlüsselunterschiede
- Video
- Abschluss
Vergleichstabelle
| Vergleichsgrundlage | Korrelation | Regression |
|---|---|---|
| Bedeutung | Korrelation ist eine statistische Maßnahme, die die Zusammenarbeit oder die Assoziation von zwei Variablen bestimmt. | Die Regression beschreibt, wie eine unabhängige Variable numerisch mit der abhängigen Variablen zusammenhängt. |
| Verwendung | Um eine lineare Beziehung zwischen zwei Variablen darzustellen. | An der Basis einer anderen Variablen zu passen und eine Variable zu schätzen und eine Variable zu schätzen. |
| Abhängige und unabhängige Variablen | Kein Unterschied | Beide Variablen sind unterschiedlich. |
| Zeigt an | Der Korrelationskoeffizient gibt an, inwieweit sich zwei Variablen zusammen bewegen. | Die Regression gibt den Einfluss einer Einheitsänderung in der bekannten Variablen (x) auf die geschätzte Variable (y) an. |
| Zielsetzung | Einen numerischen Wert zu finden, der die Beziehung zwischen Variablen ausdrückt. | Um die Werte der Zufallsvariablen anhand der Werte der festen Variablen zu schätzen. |
Definition der Korrelation
Der Begriff Korrelation ist eine Kombination von zwei Wörtern 'CO' (zusammen) und Beziehung (Verbindung) zwischen zwei Größen. Die Korrelation ist, wenn zum Zeitpunkt der Untersuchung von zwei Variablen beobachtet wird, dass eine Änderung der Einheiten in einer Variablen durch eine äquivalente Änderung in einer anderen Variablen revanchiert wird, i.e. direkt oder indirekt. Oder die Variablen sollen nicht korreliert werden, wenn die Bewegung in einer Variablen keine Bewegung in einer anderen Variablen in einer bestimmten Richtung darstellt. Es ist eine statistische Technik, die die Stärke der Verbindung zwischen Variablenpaaren darstellt.
Korrelation kann positiv oder negativ sein. Wenn sich die beiden Variablen in die gleiche Richtung bewegen, i.e. Eine Erhöhung einer Variablen führt zu einer entsprechenden Erhöhung einer anderen Variablen und umgekehrt, dann werden die Variablen als positiv korreliert angesehen. Zum Beispiel: Gewinn und Investition.
Im Gegenteil, wenn sich die beiden Variablen in unterschiedliche Richtungen bewegen, so dass eine Erhöhung einer Variablen zu einer Abnahme einer anderen Variablen führt und umgekehrt, wird diese Situation als negative Korrelation bezeichnet. Zum Beispiel: Preis und Nachfrage eines Produkts.
Die Korrelationsmaßnahmen sind wie unter:
- Karl Pearsons Produktmoment-Korrelationskoeffizient
- Spearmans Rangkorrelationskoeffizient
- Streudiagramm
- Koeffizient der gleichzeitigen Abweichungen
Definition der Regression
Eine statistische Technik zur Schätzung der Änderung der metrischen abhängigen Variablen aufgrund der Änderung einer oder mehrerer unabhängiger Variablen, basierend auf der durchschnittlichen mathematischen Beziehung zwischen zwei oder mehr Variablen, wird als Regression bezeichnet. Es spielt bei vielen menschlichen Aktivitäten eine wichtige Rolle, da es ein leistungsstarkes und flexibles Instrument ist, das die Vergangenheit, gegenwärtigen oder zukünftigen Ereignisse auf der Grundlage früherer oder gegenwärtiger Ereignisse vorhersagte. Zum Beispiel: Auf der Grundlage früherer Aufzeichnungen kann der zukünftige Gewinn eines Unternehmens geschätzt werden.
In einer einfachen linearen Regression gibt es zwei Variablen x und y, wobei y auf x abhängt oder von x beeinflusst wird. Hier wird y als abhängig oder als Kriterienvariable bezeichnet und X ist unabhängig oder Prädiktorvariable. Die Regressionslinie von y auf x wird als unter ausgedrückt:
y = a + bx
wo, a = konstant,
B = Regressionskoeffizient,
In dieser Gleichung sind A und B der zwei Regressionsparameter.
Schlüsselunterschiede zwischen Korrelation und Regression
Die nachstehend angegebenen Punkte erklären den Unterschied zwischen Korrelation und Regression im Detail:
- Eine statistische Maßnahme, die die Mitbeziehung oder Assoziation von zwei Größen bestimmt, wird als Korrelation bezeichnet. Die Regression beschreibt, wie eine unabhängige Variable numerisch mit der abhängigen Variablen zusammenhängt.
- Korrelation wird verwendet, um die lineare Beziehung zwischen zwei Variablen darzustellen. Im Gegenteil wird die Regression verwendet, um die beste Linie anzupassen und eine Variable auf der Grundlage einer anderen Variablen abzuschätzen.
- In der Korrelation gibt es keinen Unterschied zwischen abhängigen und unabhängigen Variablen i.e. Die Korrelation zwischen x und y ähnelt Y und X. Umgekehrt unterscheidet sich die Regression von y auf x von x auf y.
- Die Korrelation zeigt die Stärke der Assoziation zwischen Variablen an. Im Gegensatz zu der Regression spiegelt die Regression die Auswirkungen der Einheitsänderung in der unabhängigen Variablen auf die abhängige Variable wider.
- Die Korrelation zielt darauf ab, einen numerischen Wert zu finden, der die Beziehung zwischen Variablen ausdrückt. Im Gegensatz zu Regression, dessen Ziel es ist, Werte der Zufallsvariablen auf der Grundlage der Werte der festen Variablen vorherzusagen.
Video: Korrelation gegen Regression
Abschluss
Bei der obigen Diskussion ist offensichtlich, dass es einen großen Unterschied zwischen diesen beiden mathematischen Konzepten gibt, obwohl diese beiden gemeinsam untersucht werden. Korrelation wird verwendet, wenn der Forscher wissen möchte, ob die untersuchten Variablen korreliert sind oder nicht, wenn ja, was ist dann die Stärke ihrer Assoziation?. Der Korrelationskoeffizient von Pearson wird als das beste Maß für die Korrelation angesehen. In der Regressionsanalyse wird eine funktionale Beziehung zwischen zwei Variablen festgelegt, um zukünftige Projektionen zu Ereignissen vorzunehmen.
- « Unterschied zwischen Joint Venture und Strategic Alliance
- Unterschied zwischen formativer und summativer Bewertung »

