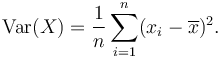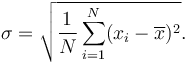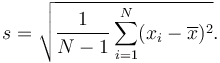Standardabweichung vs. Varianz
- 3243
- 378
- Leonhard Lesch
Standardabweichung Und Varianz sind statistische Maßnahmen zur Verteilung von Daten, ich.e., Sie repräsentieren, wie viel Variation es vom Durchschnitt gibt, oder inwieweit die Werte normalerweise vom Mittelwert (Durchschnitt) "abweichen". Eine Varianz oder Standardabweichung von Null zeigt an, dass alle Werte identisch sind.
Varianz ist der Mittelwert der Quadrate der Abweichungen (i.e., Werteunterschiede aus dem Mittelwert), und die Standardabweichung ist die Quadratwurzel dieser Varianz. Standardabweichung wird verwendet, um Ausreißer in den Daten zu identifizieren.
Vergleichstabelle
Unterschiede - Ähnlichkeiten -| Standardabweichung | Varianz | |
|---|---|---|
| Mathematische Formel | Quadratwurzel der Varianz | Durchschnitt der Quadrate der Abweichungen jedes Wertes vom Mittelwert in einer Stichprobe. |
| Symbol | Griechischer Buchstabe Sigma - σ | Kein spezielles Symbol; ausgedrückt in Bezug auf Standardabweichung oder andere Werte. |
| Werte in Bezug auf den bestimmten Datensatz | Gleiche Skala wie Werte im angegebenen Datensatz; daher in denselben Einheiten ausgedrückt. | Skalierung größer als die Werte im angegebenen Datensatz; nicht in derselben Einheit wie die Werte selbst ausgedrückt. |
| Sind Werte negativ oder positiv? | Immer nicht negativ | Immer nicht negativ |
| Real World Application | Bevölkerungstichproben; Ausreißer identifizieren | Statistische Formeln, Finanzierung. |
Wichtige Konzepte
- Bedeuten: Der Durchschnitt aller Werte in einem Datensatz (Fügen Sie alle Werte hinzu und teilen Sie ihre Summe durch die Anzahl der Werte).
- Abweichung: die Entfernung jedes Wertes vom Mittelwert. Wenn der Mittelwert 3 ist, hat ein Wert von 5 eine Abweichung von 2 (subtrahieren Sie den Mittelwert vom Wert). Abweichung kann positiv oder negativ sein.
Symbole
Die Formel für Standardabweichung und Varianz wird häufig unter Verwendung:
- x̅ = der Mittelwert oder Durchschnitt aller Datenpunkte im Problem
- X = ein einzelner Datenpunkt
- N = die Anzahl der Punkte im Datensatz
- ∑ = die Summe der [die Quadrate der Abweichungen]
Formeln
Die Varianz eines Satzes von N Ebenso wahrscheinlich können Werte geschrieben werden als:
Die Standardabweichung ist die Quadratwurzel der Varianz:
Formeln mit griechischen Buchstaben haben eine Möglichkeit, entmutigend auszusehen, aber dies weniger kompliziert als es scheint. Um es in einfache Schritte zu setzen:
- Ermitteln Sie den Durchschnitt aller Datenpunkte
- Finden Sie heraus, wie weit jeder Punkt vom Durchschnitt entfernt ist (dies ist die Abweichung)
- Senden Sie jede Abweichung (ich.e. die Differenz jedes Werts vom Mittelwert)
- Teilen Sie die Summe der Quadrate durch die Anzahl der Punkte.
Das gibt die Varianz. Nehmen Sie die Quadratwurzel der Varianz, um die Standardabweichung zu finden.
Dieses hervorragende Video der Khan Academy erklärt die Konzepte der Varianz und der Standardabweichung:
Beispiel
Nehmen wir an, ein Datensatz enthält die Höhe von sechs Löwenzahn: 3 Zoll, 4 Zoll, 5 Zoll, 4 Zoll, 11 Zoll und 6 Zoll.
Ermitteln Sie zunächst den Mittelwert der Datenpunkte: (3 + 4 + 5 + 4 + 11 + 7) / 6 = 5.5
Die mittlere Höhe beträgt also 5.5 Zoll. Jetzt brauchen wir die Abweichungen, also finden wir den Unterschied jeder Pflanze aus dem Mittelwert: -2.5, -1.5, -.5, -1.5, 5.5, 1.5
Quellen Sie jetzt jede Abweichung und finden Sie ihre Summe: 6.25 + 2.25 + .25 + 2.25 + 30.25 + 2.25 = 43.5
Teilen Sie nun die Summe der Quadrate durch die Anzahl der Datenpunkte, in diesem Fall Pflanzen: 43.5/6 = 7.25
Die Varianz dieses Datensatzes beträgt also 7.25, was eine ziemlich willkürliche Zahl ist. Um es in eine reale Messung umzuwandeln, nehmen Sie die Quadratwurzel von 7.25, um die Standardabweichung in Zoll zu finden.
Die Standardabweichung beträgt ungefähr 2.69 Zoll. Das bedeutet, dass für die Probe jeder Löwenzahn innerhalb von 2.69 Zoll des Mittelwerts (5.5 Zoll) ist "normal".
Warum die Abweichungen quadrieren?
Abweichungen werden quadratisch, um negative Werte (Abweichungen unter dem Mittelwert) zu verhindern, die positiven Werte abzubrechen. Dies funktioniert, weil eine negative Anzahl quadratisch zu einem positiven Wert wird. Wenn Sie einen einfachen Datensatz mit Abweichungen vom Mittelwert von +5, +2, -1 und -6 hatten, wird die Summe der Abweichungen als Null herausgestellt, wenn die Werte nicht quadratisch sind (ich.e. 5 + 2 - 1 - 6 = 0).
Anwendungen der realen Welt
Die Varianz wird als mathematische Dispersion ausgedrückt. Da es sich um eine willkürliche Zahl relativ zu den ursprünglichen Messungen des Datensatzes handelt, ist es schwierig, in realer Sinne visualisieren und anzuwenden. Das Finden der Varianz ist normalerweise nur der letzte Schritt, bevor Sie die Standardabweichung finden. Varianzwerte werden manchmal in Finanz- und statistischen Formeln verwendet.
Standardabweichung, die in den ursprünglichen Einheiten des Datensatzes ausgedrückt wird, ist viel intuitiver und näher an den Werten des Originaldatensatzes. Es wird am häufigsten verwendet, um Demografie oder Bevölkerungsproben zu analysieren, um ein Gefühl dafür zu gewinnen, was in der Bevölkerung normal ist.
Ausreißer finden
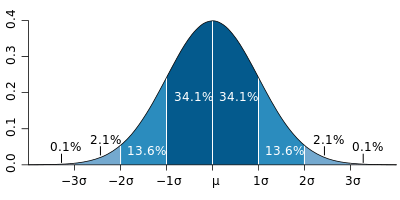Eine Normalverteilung (Glockenkurve) mit Bändern, die 1σ entsprechen In einer Normalverteilung fallen etwa 68% der Bevölkerung (oder Werte) innerhalb von 1 Standardabweichung (1σ) des Mittelwerts und etwa 94% innerhalb von 2σ fallen. Werte, die sich vom Mittelwert um 1 unterscheiden.7σ oder mehr werden normalerweise als Ausreißer betrachtet.
In der Praxis versuchen Qualitätssysteme wie Six Sigma, die Fehlerrate zu verringern, damit Fehler ein Ausreißer werden. Der Begriff "Six Sigma -Prozess" ergibt sich aus der Vorstellung, dass, wenn man sechs Standardabweichungen zwischen dem Prozessmittelwert und der nächsten Spezifikationsgrenze hat, praktisch keine Elemente die Spezifikationen nicht erfüllen können.[1]
Beispiel Standardabweichung
In realen Anwendungen repräsentieren die verwendeten Datensätze in der Regel Bevölkerungsproben und nicht in ganzen Populationen. Eine leicht modifizierte Formel wird verwendet, wenn bevölkerungsweite Schlussfolgerungen aus einer Teilprobe gezogen werden sollen.
Es wird eine „Beispiel -Standardabweichung“ verwendet, wenn Sie nur eine Stichprobe haben, aber Sie möchten eine Erklärung zur Bevölkerungsstandardabweichung abgeben, aus der die Stichprobe gezogen wird
Die einzige Möglichkeit, wie die Standardabweichungsformel der Probe von der Standardabweichungsformel unterscheidet, ist die „-1“ im Nenner.
Unter Verwendung des Dandelionsbeispiels wäre diese Formel benötigt, wenn wir nur 6 Löwenzahn abtechen würden, diese Probe jedoch verwenden wollten, um die Standardabweichung für das gesamte Feld mit Hunderten von Schuppen zu sagen.
Die Summe der Quadrate würde jetzt durch 5 anstelle von 6 (n - 1) geteilt, was eine Varianz von 8 ergibt.7 (statt 7.25) und eine Stichprobenstandardabweichung von 2.95 Zoll statt 2.69 Zoll für die ursprüngliche Standardabweichung. Diese Änderung wird verwendet, um in einer Stichprobe einen Fehlerrand zu finden (9% in diesem Fall).