Unterschied zwischen Varianz und Standardabweichung

- 3338
- 236
- Hr. Jeremie Orth
 Die Dispersion gibt an, inwieweit Beobachtungen von einem geeigneten Maß für die zentrale Tendenz abweichen. Messungen der Dispersion fallen in zwei Kategorien I.e. Ein absolutes Maß für Dispersion und relatives Maß für die Dispersion. Varianz und Standardabweichung sind zwei Arten eines absoluten Maßes für die Variabilität. Das beschreibt, wie sich die Beobachtungen um den Mittelwert ausbreiten. Varianz ist nichts als der Durchschnitt der Quadrate der Abweichungen,
Die Dispersion gibt an, inwieweit Beobachtungen von einem geeigneten Maß für die zentrale Tendenz abweichen. Messungen der Dispersion fallen in zwei Kategorien I.e. Ein absolutes Maß für Dispersion und relatives Maß für die Dispersion. Varianz und Standardabweichung sind zwei Arten eines absoluten Maßes für die Variabilität. Das beschreibt, wie sich die Beobachtungen um den Mittelwert ausbreiten. Varianz ist nichts als der Durchschnitt der Quadrate der Abweichungen,
nicht wie, Standardabweichung ist die Quadratwurzel des numerischen Wertes, der bei der Berechnung der Varianz erhalten wird. Viele Menschen kontrastieren diese beiden mathematischen Konzepte. Dieser Artikel versucht also, den wichtigen Unterschied zwischen Varianz und Standardabweichung aufzutragen.
Inhalt: Varianz gegen Standardabweichung
- Vergleichstabelle
- Definition
- Schlüsselunterschiede
- Illustration
- Ähnlichkeiten
- Abschluss
Vergleichstabelle
| Vergleichsgrundlage | Varianz | Standardabweichung |
|---|---|---|
| Bedeutung | Varianz ist ein numerischer Wert, der die Variabilität von Beobachtungen aus ihrem arithmetischen Mittelwert beschreibt. | Standardabweichung ist ein Maß für die Dispersion von Beobachtungen innerhalb eines Datensatzes. |
| Was ist es? | Es ist der Durchschnitt der quadratischen Abweichungen. | Es ist die Wurzel mittlere quadratische Abweichung. |
| Bezeichnet als | Sigma-Quadrat (σ^2) | Sigma (σ) |
| Ausgedrückt | Quadratische Einheiten | Gleiche Einheiten wie die Werte im Datensatz. |
| Zeigt an | Wie weit Menschen in einer Gruppe verteilt sind. | Wie viel Beobachtungen eines Datensatzes unterscheiden sich von seinem Mittelwert von seinem Mittelwert. |
Definition der Varianz
In der Statistik wird die Varianz als das Maß für die Variabilität definiert, die darstellt, wie weit die Mitglieder einer Gruppe verteilt sind. Es findet heraus, dass durchschnittlich Grad, in dem jede Beobachtung vom Mittelwert variiert. Wenn die Varianz eines Datensatzes gering ist, zeigt dies die Nähe der Datenpunkte auf den Mittelwert, während ein größerer Varianzwert darstellt.
Für nicht klassifizierte Daten: 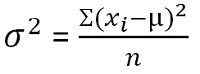
Für gruppierte Frequenzverteilung: 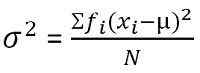
Definition der Standardabweichung
Standardabweichung ist eine Maßnahme, die die Dispersion der Beobachtungen in einem Datensatz quantifiziert. Die niedrige Standardabweichung ist ein Indikator für die Nähe der Bewertungen zum arithmetischen Mittelwert, und eine hohe Standardabweichung repräsentiert; Die Bewertungen werden über einen höheren Wertebereich verteilt.
Für nicht klassifizierte Daten: 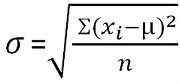 Für gruppierte Frequenzverteilung:
Für gruppierte Frequenzverteilung: 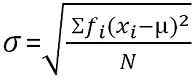
Schlüsselunterschiede zwischen Varianz und Standardabweichung
Der Unterschied zwischen Standardabweichung und Varianz kann aus den folgenden Gründen klar gezeichnet werden:
- Varianz ist ein numerischer Wert, der die Variabilität von Beobachtungen aus ihrem arithmetischen Mittelwert beschreibt. Standardabweichung ist ein Maß für die Dispersion von Beobachtungen innerhalb eines Datensatzes im Vergleich zu ihrem Mittelwert.
- Varianz ist nichts anderes als ein Durchschnitt der quadratischen Abweichungen. Andererseits ist die Standardabweichung die mittlere quadratische Abweichung.
- Die Varianz wird durch Sigma-Quadrat (σ) bezeichnet2) Während die Standardabweichung als Sigma (σ) gekennzeichnet ist.
- Die Varianz wird in quadratischen Einheiten ausgedrückt, die normalerweise größer sind als die Werte im angegebenen Datensatz. Im Gegensatz zur Standardabweichung, die in denselben Einheiten wie die Werte im Datensatz ausgedrückt wird.
- Varianz misst, wie weit Einzelpersonen in einer Gruppe im Datensatz aus dem Durchschnitt verteilt sind. Umgekehrt misst die Standardabweichung, wie viel Beobachtungen eines Datensatzes von seinem Mittelwert unterschiedlich sind.
Illustration
Markierungen, die von einem Studenten in fünf Fächern erzielt wurden, sind 60, 75, 46, 58 bzw. 80. Sie müssen die Standardabweichung und Varianz herausfinden.
Zunächst müssen Sie den Mittelwert herausfinden,
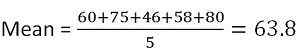
Die durchschnittlichen (mittleren) Markierungen betragen also 63.8
Berechnen Sie nun die Varianz
| X | A | (x-a) | (X-a)^2 |
|---|---|---|---|
| 60 | 63.8 | -3.8 | 14.44 |
| 75 | 63.8 | 11.2 | 125.44 |
| 46 | 63.8 | -17.8 | 316.84 |
| 58 | 63.8 | 5.8 | 33.64 |
| 80 | 63.8 | 16.2 | 262.44 |
Wo, x = Beobachtungen
A = arithmetischer Mittelwert
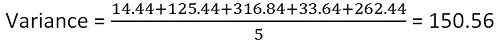 Die Varianz beträgt also 150.56
Die Varianz beträgt also 150.56
Und Standardabweichung ist - 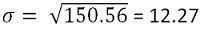
Ähnlichkeiten
- Sowohl Varianz als auch Standardabweichung sind immer positiv.
- Wenn alle Beobachtungen in einem Datensatz identisch sind, sind die Standardabweichung und Varianz Null.
Abschluss
Diese beiden sind grundlegende statistische Begriffe, die in verschiedenen Sektoren eine wichtige Rolle spielen. Die Standardabweichung wird gegenüber dem Mittelwert bevorzugt, da sie in denselben Einheiten wie die der Messungen ausgedrückt wird, während die Varianz in den Einheiten, die größer als der angegebene Datensatz sind, ausgedrückt wird.

