Unterschied zwischen T-Test und F-Test

- 921
- 172
- Milana Battke
 Hypothesentests beginnt mit der Einrichtung der Räumlichkeiten, gefolgt von der Auswahl einer Signifikanzstufe. Als nächstes müssen wir die Teststatistik auswählen, ich.e. T-Test oder F-Test. Während T-Test wird verwendet, um zwei verwandte Proben zu vergleichen, F-Test wird verwendet, um die Gleichheit von zwei Populationen zu testen.
Hypothesentests beginnt mit der Einrichtung der Räumlichkeiten, gefolgt von der Auswahl einer Signifikanzstufe. Als nächstes müssen wir die Teststatistik auswählen, ich.e. T-Test oder F-Test. Während T-Test wird verwendet, um zwei verwandte Proben zu vergleichen, F-Test wird verwendet, um die Gleichheit von zwei Populationen zu testen.
Die Hypothese ist ein einfacher Satz, der durch verschiedene wissenschaftliche Techniken nachgewiesen oder widerlegt werden kann und die Beziehung zwischen unabhängiger und einigen abhängigen Variablen herstellt. Es ist in der Lage, durch eine unvoreingenommene Prüfung getestet und verifiziert zu werden, um seine Gültigkeit festzustellen. Testen einer Hypotheseversuche, um klar zu machen, ob die Annahme gültig ist oder nicht.
Für einen Forscher ist es unerlässlich, den richtigen Test für seine Hypothese als die gesamte Entscheidung, die Nullhypothese zu validieren oder abzulehnen, zu wählen. Lesen Sie den angegebenen Artikel, um den Unterschied zwischen T-Test und F-Test zu verstehen.
Inhalt: T-Test gegen F-Test
- Vergleichstabelle
- Definition
- Schlüsselunterschiede
- Abschluss
Vergleichstabelle
| Vergleichsgrundlage | T-Test | F-Test |
|---|---|---|
| Bedeutung | T-Test ist ein univariater Hypothesentest, der angewendet wird, wenn die Standardabweichung nicht bekannt ist und die Stichprobengröße klein ist. | F-Test ist statistischer Test, der die Gleichheit der Varianzen der beiden normalen Populationen bestimmt. |
| Teststatistik | T-Statistik folgt die T-Verteilung der Schüler unter Nullhypothese. | F-Statistik folgt SNEDECOR F-Distribution unter Nullhypothese. |
| Anwendung | Vergleich der Mittelwerte von zwei Populationen. | Vergleich von zwei Bevölkerungsvarianzen. |
Definition des T-Tests
Ein T-Test ist eine Form des statistischen Hypothesentests, der auf T-Statistik und T-Verteilung des Schülers basiert, um den p-Wert (Wahrscheinlichkeit) herauszufinden, mit dem die Nullhypothese akzeptiert oder abgelehnt werden kann.
T-Test-Analysen, wenn sich die Mittelwerte von zwei Datensätzen stark voneinander unterscheiden, i.e. Ob der Bevölkerungsmittelwert gleich oder unterscheidet sich vom Standardmittelwert. Es kann auch verwendet werden, um festzustellen, ob die Regressionslinie eine andere Steigung von Null hat. Der Test basiert auf einer Reihe von Annahmen, die::
- Die Bevölkerung ist unendlich und normal.
- Die Populationsvarianz ist unbekannt und aus der Stichprobe geschätzt.
- Der Mittelwert ist bekannt.
- Probenbeobachtungen sind zufällig und unabhängig.
- Die Probengröße ist klein.
- H0 kann einseitig oder zweiseitig sein.
Mittelwert und Standardabweichung der beiden Stichproben werden verwendet, um einen Vergleich zwischen ihnen zu machen, so dass:
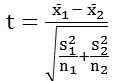 Wo,
Wo,
X1 = Mittelwert des ersten Datensatzes
x̄2 = Mittelwert des zweiten Datensatzes
S1 = Standardabweichung des ersten Datensatzes
S2 = Standardabweichung des zweiten Datensatzes
N1 = Größe des ersten Datensatzes
N2 = Größe des zweiten Datensatzes
Definition des F-Tests
Der F-Test wird als eine Art Hypothesentest beschrieben, der auf der Nullhypothese auf der Nullhypothese basiert. Der Test wird durchgeführt, wenn nicht bekannt ist, ob die beiden Populationen die gleiche Varianz haben.
Der F-Test kann auch verwendet werden, um zu überprüfen, ob die Daten einem Regressionsmodell entsprechen, das durch die kleinste Quadratanalyse erfasst wird. Wenn eine mehrfache lineare Regressionsanalyse vorliegt, wird die Gesamtvalidität des Modells untersucht oder festgelegt, ob eine der unabhängigen Variablen eine lineare Beziehung zur abhängigen Variablen hat. Eine Reihe von Vorhersagen kann durch den Vergleich der beiden Datensätze getroffen werden. Die Expression des F-Testwerts liegt im Verhältnis von Varianzen der beiden Beobachtungen, die als unter dargestellt sind:
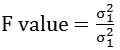 Wo, σ2 = Varianz
Wo, σ2 = Varianz
Die Annahmen, auf die sich F-Test stützt, sind:
- Die Bevölkerung ist normal verteilt.
- Proben wurden zufällig gezeichnet.
- Beobachtungen sind unabhängig.
- H0 kann einseitig oder zweiseitig sein.
Schlüsselunterschiede zwischen T-Test und F-Test
Der Unterschied zwischen T-Test und F-Test kann aus den folgenden Gründen klar gezeichnet werden:
- Ein univariater Hypothesentest, der angewendet wird, wenn die Standardabweichung nicht bekannt ist und die Stichprobengröße klein ist, ist ein T-Test. Andererseits wird ein statistischer Test, der die Gleichheit der Varianzen der beiden normalen Datensätze bestimmt, als F-Test bezeichnet.
- Der T-Test basiert auf T-Statistik folgt die T-Verteilung der Schüler unter der Nullhypothese. Umgekehrt folgt die Grundlage des F-Tests F-Statistik unter der Nullhypothese Snedecor F-Distribution.
- Der T-Test wird verwendet, um die Mittelwerte von zwei Populationen zu vergleichen. Im Gegensatz dazu wird der F-Test verwendet, um zwei Populationsvarianzen zu vergleichen.
Abschluss
T-Test und F-Test sind die beiden, von der Anzahl der verschiedenen Arten von statistischen Tests, die für Hypothesentests verwendet werden, und entscheiden, ob wir die Nullhypothese akzeptieren oder ablehnen wollen. Der Hypothesentest trifft keine Entscheidungen selbst, sondern hilft dem Forscher bei der Entscheidungsfindung.
- « Unterschied zwischen parametrischer und nichtparametrischer Test
- Unterschied zwischen Varianz und Standardabweichung »

