Unterschied zwischen Union und Kreuzung

Bevor Sie den Unterschied zwischen den beiden festgelegten Operatoren Union und Kreuzung verstehen, verstehen wir zunächst das Konzept der Set -Theorie. Die festgelegte Theorie ist ein grundlegender Zweig der Mathematik, der untersucht, insbesondere ob ein Objekt zu einer Reihe von Objekten gehört oder nicht zu einer Reihe von Objekten, die irgendwie relevante Mathematik sind. Das SET ist im Grunde eine Sammlung gut definierter Objekte, die von mathematischer Relevanz wie Zahlen oder Funktionen sein können oder auch nicht. Die Objekte in einem Set werden als Elemente bezeichnet, die so etwas wie Zahlen, Menschen, Autos, Staaten usw. sein können. Fast alles und eine beliebige Anzahl von Elementen kann zusammen gesammelt werden, um einen Satz zu erstellen.

In einfachen Worten ist SET eine Sammlung einer beliebigen Anzahl von ungeordneten Elementen, die als einzelnes Objekt als Ganzes angesehen werden können. Lassen Sie uns die grundlegenden Konzepte und die Notation eines Satzes und wie es dargestellt wird. Alles beginnt mit einer binären Beziehung zwischen einem Objekt X und einem Satz a. Um darzustellen, ob x ein Mitglied eines Satzes A ist, wird die Notation x ∊ A verwendet, während x ∉ A angibt, dass das Objekt X nicht zum Satz A gehört. Das Mitglied eines Sets ist in lockigen Zahnspangen aufgeführt. Zum Beispiel kann der Satz von Primzahlen von weniger als 10 als 2, 3, 5, 7 geschrieben werden. In ähnlicher Weise kann eine Reihe von geraden Zahlen von weniger als 10 als 2, 4, 6, 8 geschrieben werden. Hypothetisch kann fast jedes endliche Set von seinen Mitgliedern vertreten werden.

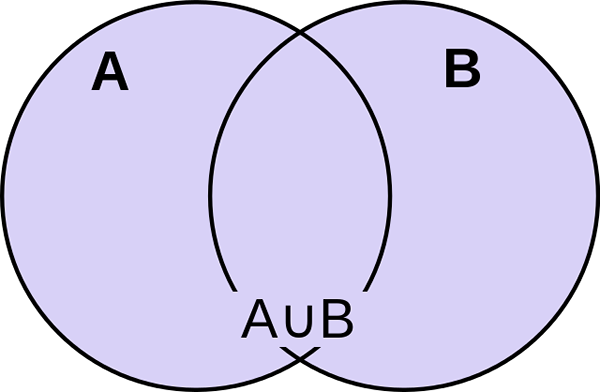
Was ist die Vereinigung von Sets?

Die Vereinigung von zwei Sätzen A und B ist definiert als die Reihe von Elementen, die entweder A oder B oder möglicherweise zu BEI gehören. Es ist einfach als die Menge aller verschiedenen Elemente oder Mitglieder definiert, bei denen die Mitglieder zu diesen Sätzen gehören. Der Gewerkschaftsbetreiber entspricht dem logischen oder und wird durch das Symbol ∪ dargestellt. Es ist der kleinste Satz, der alle Elemente beider Sets enthält. Wenn beispielsweise eingestellt ist, ist A 1, 2, 3, 4, 5 und Set B 3, 4, 6, 7, 9, dann wird die Vereinigung von A und B durch A∪B dargestellt und geschrieben als 1, 2, 3, 4, 5, 6, 7, 9. Da die Zahlen 3 und 4 in beiden Sätzen A und B vorhanden sind, müssen sie nicht zweimal aufgeführt werden. Es ist offensichtlich, dass die Anzahl der Elemente der Vereinigung von A und B kleiner ist als die Summe der einzelnen Sätze, da nur wenige Zahlen in beiden Sätzen üblich sind.

A = 1, 3, 5, 7, 9

B = 3, 6, 9, 12, 15

A∪b = 1, 3, 5, 6, 7, 9, 12, 15

Was ist Schnittpunkt der Sets?

Der Schnittpunkt von zwei Mengen A und B ist definiert als die Reihe von Elementen, die sowohl zu A als auch zu B gehören. Es ist einfach definiert als die Menge, die alle Elemente des Satzes A enthält, die auch zum Satz B gehören, und in ähnlicher Weise gehören alle Elemente von Set B zum Satz A. Der Kreuzungsoperator entspricht dem logischen und wird durch das Symbol ∩ dargestellt. Im Gegenteil ist der Schnittpunkt von zwei Sätzen der größte Satz, der alle Elemente enthält, die bei beiden Sätzen gemeinsam sind. Wenn beispielsweise ein Satz a 1, 2, 3, 4, 5 und Set B ist, ist 3, 4, 6, 7, 9, dann wird der Schnittpunkt von A und B durch A∩b dargestellt und geschrieben als 3, 4. Da nur die Zahlen 3 und 4 in beiden Mengen A und B üblich sind, werden sie als Schnittpunkt der Sets bezeichnet.

A = 2, 3, 5, 7, 11

B = 1, 3, 5, 7, 9, 11

A∩b = 3, 5, 7, 11

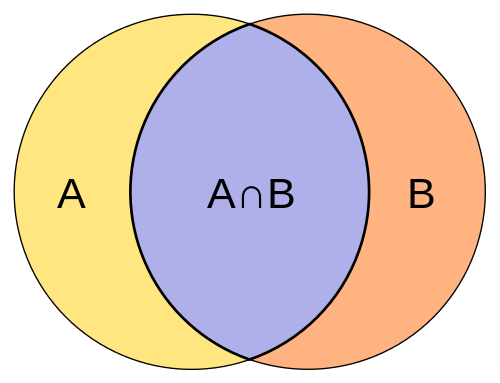
Unterschied zwischen Gewerkschaft und Schnittpunkt der Sets

1. Basic - Die Vereinigung von zwei Mengen A und B ist definiert als die Reihe von Elementen, die entweder zu A oder B oder möglicherweise beides gehören, während der Schnittpunkt von zwei Sätzen als die Reihe von Elementen definiert ist, die sowohl A als auch B gehören.
2. Symbolische Darstellung - Die Vereinigung von zwei Sätzen wird durch das Symbol „∪“ dargestellt, während der Schnittpunkt zweier Sätze durch das Symbol „∩“ dargestellt wird.
3. Logische Relevanz - Die Vereinigung von zwei Mengen entspricht dem logischen „oder“, während der Schnittpunkt zweier Sätze dem logischen „und“ entspricht.
4. Beispiel - Sei a = a, e, i, o, u und

B = a, b, c, d, e, f

A∪b = a, b, c, d, e, f, i, o, u

A∩b = a, e

Union vs. Kreuzung: Vergleichstabelle

Zusammenfassung von Union vs. Überschneidung

Sowohl Union als auch Kreuzung sind die beiden grundlegenden Operationen, durch die Sets kombiniert und miteinander verbunden werden können. In Bezug auf die festgelegte Theorie ist Union der Satz aller Elemente, die sich entweder in der SET oder in beiden befinden, während die Schnittstelle die Menge aller verschiedenen Elemente ist, die zu beiden Sätzen gehören. Die Vereinigung von zwei Mengen A und B wird als „A∪b“ symbolisiert, während die Schnittstelle von A und B als „A∩b“ symbolisiert wird. Set ist nichts anderes als eine Sammlung gut definierter Objekte wie Zahlen und Funktionen, und die Objekte in einem Satz werden als Elemente bezeichnet.