Unterschied zwischen T-Test und Z-Test

- 2844
- 250
- Rahel Diedrich
 T-Test bezieht sich auf einen univariaten Hypothesentest, der auf T-Statistik basiert, wobei der Mittelwert bekannt ist, und die Populationsvarianz von der Stichprobe annähert. Andererseits, Z-Test ist auch ein univariater Test, der auf der Standardnormalverteilung basiert.
T-Test bezieht sich auf einen univariaten Hypothesentest, der auf T-Statistik basiert, wobei der Mittelwert bekannt ist, und die Populationsvarianz von der Stichprobe annähert. Andererseits, Z-Test ist auch ein univariater Test, der auf der Standardnormalverteilung basiert.
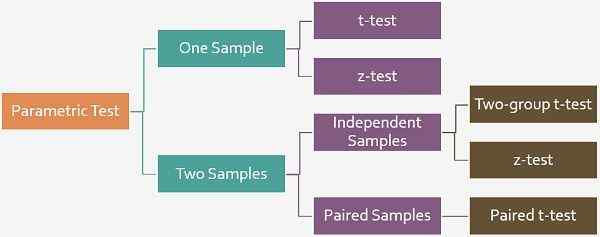
In einfachen Worten bezieht sich eine Hypothese auf eine Annahme, die akzeptiert oder abgelehnt werden soll. Es gibt zwei Hypothesentestverfahren, ich.e. parametrischer Test und nicht parametrischer Test, wobei der parametrische Test auf der Tatsache basiert, dass die Variablen auf einer Intervallskala gemessen werden, während im nicht parametrischen Test angenommen wird, dass dies auf einer Ordnungsskala gemessen wird. Jetzt können im parametrischen Test zwei Arten von Tests, T-Test und Z-Test bestehen.
In diesem Artikel wird Ihnen ein Verständnis für den Unterschied zwischen T-Test und Z-Test im Detail vermittelt.
Inhalt: T-Test gegen Z-Test
- Vergleichstabelle
- Definition
- Schlüsselunterschiede
- Abschluss
Vergleichstabelle
| Vergleichsgrundlage | T-Test | Z-Test |
|---|---|---|
| Bedeutung | T-Test bezieht. | Z-Test impliziert einen Hypothesentest, der feststellt, ob sich die Mittelwerte von zwei Datensätzen voneinander unterscheiden. |
| Bezogen auf | Student-T-Verteilung | Normalverteilung |
| Bevölkerungsvarianz | Unbekannt | Bekannt |
| Probengröße | Klein | Groß |
Definition des T-Tests
Ein T-Test ist ein Hypothesentest, der vom Forscher verwendet wird, um Populationsmittel für eine Variable zu vergleichen, die je nach weniger als Intervallvariable in zwei Kategorien eingeteilt ist. Genauer gesagt wird ein T-Test verwendet, um zu untersuchen, wie sich die Mittel aus zwei unabhängigen Proben unterscheiden.
Der T-Test folgt der T-Verteilung, was angemessen ist, wenn die Stichprobengröße gering ist und die Bevölkerungsstandardabweichung nicht bekannt ist. Die Form einer T-Verteilung ist stark vom Freiheitsgrad beeinflusst. Der Freiheitsgrad impliziert die Anzahl der unabhängigen Beobachtungen in einem bestimmten Satz von Beobachtungen.
Annahmen des T-Tests:
- Alle Datenpunkte sind unabhängig.
- Die Probengröße ist klein. Im Allgemeinen wird eine Stichprobengröße von mehr als 30 Probeneinheiten als groß, ansonsten klein angesehen, aber das sollte nicht weniger als 5 sein, um T-Test anzuwenden.
- Beispielwerte sind genau zu entnehmen und genau aufgezeichnet zu werden.
Die Teststatistik lautet:
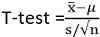
x ̅ ist der Probenmittelwert
S ist Probenstandardabweichung
n ist die Probengröße
μ ist der Bevölkerungsmittelwert
Gepaarten T-Test: Ein statistischer Test, der angewendet wird, wenn die beiden Proben abhängig sind und gepaarte Beobachtungen durchgeführt werden.
Definition des Z-Tests
Z-Test bezieht sich auf eine univariate statistische Analyse. Es bestimmt, inwieweit ein Datenpunkt in der Standardabweichung von seinem Mittelwert des Datensatzes weg ist.
Der Forscher übernimmt den Z-Test, wenn die Populationsvarianz bekannt ist, im Wesentlichen, wenn eine große Stichprobengröße vorliegt, die Stichprobenvarianz als ungefähr gleich der Populationsvarianz ist. Auf diese Weise wird angenommen, dass es bekannt ist, obwohl nur Beispieldaten verfügbar sind und so ein normaler Test angewendet werden kann.
Annahmen des Z-Tests:
- Alle Probenbeobachtungen sind unabhängig
- Die Probengröße sollte mehr als 30 betragen.
- Die Verteilung von Z ist normal, mit einem mittleren Null- und Varianz 1.
Die Teststatistik lautet:
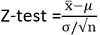
x ̅ ist der Probenmittelwert
σ ist die Bevölkerungsstandardabweichung
n ist die Probengröße
μ ist der Bevölkerungsmittelwert
Schlüsselunterschiede zwischen T-Test und Z-Test
Der Unterschied zwischen T-Test und Z-Test kann aus den folgenden Gründen klar gezeichnet werden:
- Der T-Test kann als statistischer Test verstanden werden, der zum Vergleichen und Analysieren verwendet wird, ob sich die Mittelwerte der beiden Bevölkerung voneinander unterscheiden oder nicht, wenn die Standardabweichung nicht bekannt ist. Im Gegensatz dazu ist Z-Test ein parametrischer Test, der angewendet wird, wenn die Standardabweichung bekannt ist, um festzustellen, ob sich die Mittelwerte der beiden Datensätze voneinander unterscheiden.
- Der T-Test basiert auf der T-Verteilung des Studenten. Im Gegenteil, der Z-Test beruht auf der Annahme, dass die Verteilung der Stichprobenmittelmittel normal ist. Die T-Verteilung der Schüler und die Normalverteilung erscheinen gleichermaßen, da beide symmetrisch und glockenförmig sind. Sie unterscheiden.
- Eine der wichtigsten Bedingungen für die Einführung von T-Test ist, dass die Bevölkerungsvarianz unbekannt ist. Umgekehrt sollte die Bevölkerungsvarianz im Falle eines Z-Tests als bekannt sein oder angenommen werden.
- Z-Test wird verwendet, wenn die Probengröße groß ist, ich.e. N> 30 und T-Test ist angemessen, wenn die Größe der Probe klein ist, in dem Sinne, dass n < 30.
Abschluss
Im Großen und Ganzen sind T-Test und Z-Test fast ähnliche Tests, aber die Bedingungen für ihre Anwendung sind unterschiedlich, was bedeutet, dass T-Test angemessen ist, wenn die Größe der Probe nicht mehr als 30 Einheiten beträgt. Wenn es sich jedoch um mehr als 30 Einheiten handelt, muss z-Test durchgeführt werden. In ähnlicher Weise gibt es andere Erkrankungen, die deutlich machen, dass der Test in einer bestimmten Situation durchgeführt werden soll.
- « Unterschied zwischen Feuerwehrversicherung und Meeresversicherung
- Unterschied zwischen Audit und Bewertung »

