Unterschied zwischen Permutation und Kombination

- 2003
- 615
- Prof. Dr. Dylan Hentschel
 In der Mathematik haben Sie vielleicht die Begriffe der Permutation und der Kombination von Male gehört, aber haben Sie sich jemals vorgestellt, dass diese beiden unterschiedlichen Konzepte sind? Der grundlegende Unterschied zwischen Permutation und Kombination ist die Reihenfolge der Objekte, in Permutation Die Reihenfolge der Objekte ist sehr wichtig, ich.e. Die Anordnung muss sich in der festgelegten Reihenfolge der Anzahl der Objekte befinden, die nur einige oder alle gleichzeitig eingenommen haben.
In der Mathematik haben Sie vielleicht die Begriffe der Permutation und der Kombination von Male gehört, aber haben Sie sich jemals vorgestellt, dass diese beiden unterschiedlichen Konzepte sind? Der grundlegende Unterschied zwischen Permutation und Kombination ist die Reihenfolge der Objekte, in Permutation Die Reihenfolge der Objekte ist sehr wichtig, ich.e. Die Anordnung muss sich in der festgelegten Reihenfolge der Anzahl der Objekte befinden, die nur einige oder alle gleichzeitig eingenommen haben.
Dagegen im Fall von a Kombination, Die Bestellung spielt überhaupt keine Rolle. Nicht nur in der Mathematik, sondern auch im praktischen Leben werden wir diese beiden Konzepte regelmäßig durchmachen. Obwohl wir es nie bemerken, bemerken wir es nie. Lesen Sie den Artikel sorgfältig aus, um zu wissen, wie unterschiedlich diese beiden Konzepte unterschiedlich sind.
Inhalt: Permutation gegen Kombination
- Vergleichstabelle
- Definition
- Schlüsselunterschiede
- Beispiel
- Abschluss
Vergleichstabelle
| Vergleichsgrundlage | Permutation | Kombination |
|---|---|---|
| Bedeutung | Permutation bezieht. | Die Kombination bezieht sich auf verschiedene Möglichkeiten, Elemente aus einer großen Reihe von Objekten auszuwählen, so dass ihre Bestellung keine Rolle spielt. |
| Befehl | Relevant | Irrelevant |
| Bezeichnet | Anordnung | Auswahl |
| Was ist es? | Bestellte Elemente | Ungeordnete Sets |
| Antworten | Wie viele verschiedene Anordnungen können aus einem bestimmten Satz von Objekten erstellt werden? | Wie viele verschiedene Gruppen können aus einer größeren Gruppe von Objekten ausgewählt werden? |
| Ableitung | Multiple Permutation aus einer einzigen Kombination. | Einzelne Kombination aus einer einzelnen Permutation. |
Definition der Permutation
Wir definieren die Permutation als unterschiedliche Möglichkeiten, einige oder alle Mitglieder eines Sets in einer bestimmten Reihenfolge zu arrangieren. Es impliziert die mögliche Anordnung oder Neuordnung des angegebenen Satzes in eine unterscheidbare Reihenfolge.
Zum Beispiel, Alle möglichen Permutation mit Buchstaben x, y, z erstellt -
- Indem Sie alle drei gleichzeitig nehmen, sind XYZ, XZY, YXZ, YZX, ZXY, ZYX.
- Durch die jeweilige Zeit sind XY, XZ, YX, YZ, ZX, ZY.
Die Gesamtzahl der möglichen Permutationen von N -Dingen, die jeweils aufgenommen wurden, können berechnet werden als:
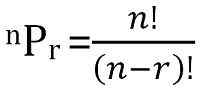
Definition der Kombination
Die Kombination ist definiert als die unterschiedlichen Möglichkeiten, eine Gruppe auszuwählen, indem einige oder alle Mitglieder eines Satzes ohne die folgende Reihenfolge genommen werden.
Zum Beispiel, Alle möglichen Kombinationen, die mit Buchstaben M, n, o ausgewählt wurden -
- Wenn drei von drei Buchstaben ausgewählt werden sollen, dann ist die einzige Kombination MNO
- Wenn zwei von drei Buchstaben ausgewählt werden sollen, sind die möglichen Kombinationen Mn, nein, om.
Die Gesamtzahl der möglichen Kombinationen von N -Dingen, die R nach einem Zeitpunkt aufgenommen haben, kann berechnet werden als:
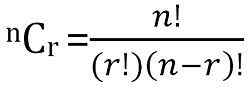
Schlüsselunterschiede zwischen Permutation und Kombination
Die Unterschiede zwischen Permutation und Kombination werden aus den folgenden Gründen deutlich gezeichnet:
- Der Begriff Permutation bezieht sich auf verschiedene Möglichkeiten, eine Reihe von Objekten in einer sequentiellen Reihenfolge zu ordnen. Kombination impliziert verschiedene Möglichkeiten, Elemente aus einem großen Pool von Objekten auszuwählen, so dass ihre Ordnung irrelevant ist.
- Der primäre Unterscheidungspunkt zwischen diesen beiden mathematischen Konzepten ist Ordnung, Platzierung und Position, i.e. In den oben genannten Permutationsmerkmalen ist wichtig, was bei der Kombination keine Rolle spielt.
- Permutation bezeichnet verschiedene Möglichkeiten, Dinge, Menschen, Ziffern, Alphabete, Farben usw. zu arrangieren. Auf der anderen Seite zeigt die Kombination verschiedene Möglichkeiten zur Auswahl von Menüpunkten, Essen, Kleidung, Probanden usw. an.
- Die Permutation ist nichts anderes als eine geordnete Kombination, während die Kombination ungeordnete Sätze oder eine Paarung von Werten innerhalb bestimmter Kriterien impliziert.
- Viele Permutationen können aus einer einzigen Kombination abgeleitet werden. Umgekehrt kann nur eine einzige Kombination aus einer einzelnen Permutation erhalten werden.
- Permutation beantwortet, wie viele verschiedene Arrangements aus einem bestimmten Satz von Objekten erstellt werden können? Im Gegensatz zu der Kombination, die erklärt, wie viele verschiedene Gruppen aus einer größeren Gruppe von Objekten ausgewählt werden können?
Beispiel
Angenommen, es gibt eine Situation, in der Sie die Gesamtzahl möglicher Stichproben von zwei von drei Objekten A, B, C herausfinden müssen. In dieser Frage müssen Sie zunächst verstehen, ob sich die Frage auf Permutation oder Kombination bezieht und dies nur herausfinden kann, ob die Bestellung wichtig ist oder nicht.
Wenn die Reihenfolge erheblich ist, bezieht sich die Frage auf die Permutation, und mögliche Proben sind AB, BA, BC, CB, AC, CA, CA. Wo, AB unterscheidet sich von BA, BC unterscheidet sich von CB und AC ist unterschiedlich ca.
Wenn die Reihenfolge irrelevant ist, bezieht sich die Frage auf die Kombination, und die möglichen Stichproben sind AB, BC und CA.
Abschluss
Bei der obigen Diskussion ist klar, dass Permutation und Kombination unterschiedliche Begriffe sind, die in Mathematik, Statistiken, Forschung und unserem täglichen Leben verwendet werden. Ein Punkt, an den sich diese beiden Konzepte erinnern, ist, dass die Permutation für eine bestimmte Reihe von Objekten immer höher ist als ihre Kombination.
- « Unterschied zwischen Buchhaltung und Prüfung
- Unterschied zwischen Joint Venture und Strategic Alliance »

