Unterschied zwischen Parabola und Hyperbel

Parabola gegen Hyperbel

Parabola und Hyperbel sind zwei verschiedene Abschnitte eines Kegels. Wir können mit ihren Unterschieden in einer mathematischen Erklärung umgehen oder mit den Unterschieden auf sehr einfache Weise umgehen, die nicht nur Mathematiker, sondern jeder verstehen kann. Dieser Artikel wird versuchen, den Unterschied zwischen ihnen auf sehr einfache Weise zu erklären.
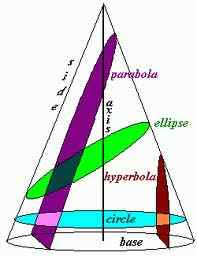
Erstens, wenn eine feste Figur, die in diesem Fall ein Kegel ist, von einer Ebene geschnitten wird, wird der erhaltene Abschnitt als Kegelabschnitt bezeichnet. Konic -Schnitte könnten Kreise, Ellipsen, Hyperbolas und Parabel sein, abhängig vom Schnittwinkel zwischen der Achse des Kegels und der Ebene. Sowohl Parabolas als auch Hyperbolas sind eine offene Kurve, was bedeutet, dass die Arme oder Zweige der Kurven weiterhin unendlich sind; Sie sind keine geschlossenen Kurven wie ein Kreis oder eine Ellipse.

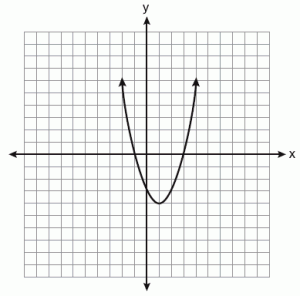
Parabel
Eine Parabola ist die Kurve, die erhalten wird, wenn die Ebene parallel zur Kegelseite schneidet. In einer Parabola wird eine Linie, die den Fokus und senkrecht zum Directrix durchläuft, als „Achse der Symmetrie.Wenn die Parabel durch den Punkt auf der „Achse der Symmetrie“ durchschnitten wird, wird sie als „Scheitelpunkt“ bezeichnet.„Alle Parabel sind identisch geformt, wenn sie in einem bestimmten Winkel geschnitten werden. Es ist eine durch die Exzentrizität von „1.Dies ist der Grund, warum sie alle gleiche Form haben, aber von verschiedenen Größen sein können.

Die Parabola wird durch die Gleichung y2 = x gegeben
Wenn eine Menge von Punkten, die in einer Ebene vorhanden sind.
Parabolas haben viele praktische Anwendungen. Sie werden zum Entwerfen des Weges von Raketen, Scheinwerferreflektoren von Automobilen, Teleskopen, Radarempfängern und Satellitenschalen verwendet.

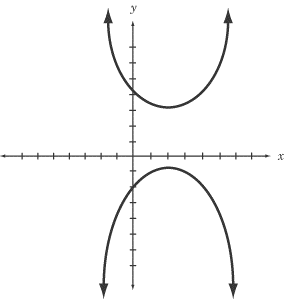
Hyperbel

Hyperbel ist die Kurve, die erhalten wird, wenn die Ebene fast parallel zur Achse schneidet. Hyperbolas sind nicht identisch, da zwischen der Achse und der Ebene viele Winkel bestehen. "Scheitelpunkte" sind die Punkte auf den beiden Armen, die am nächsten sind; Während das Liniensegment, das die Arme verbindet.”
In einer Parabola werden die beiden Arme der Kurve, auch Zweige genannt, parallel zueinander. In einer Hyperbel werden die beiden Arme oder Kurven nicht parallel. Ein Hyperbel -Zentrum ist der Mittelpunkt der Hauptachse.

Hyperbel wird durch die Gleichung xy = 1 gegeben

Wenn die Differenz der Entfernungen zwischen einer Reihe von Punkten, die in einer Ebene zu zwei festen Foki oder Punkten vorhanden sind.

Zusammenfassung:
Wenn eine Menge von Punkten, die in einer Ebene vorhanden sind. Wenn die Differenz der Entfernungen zwischen einer Reihe von Punkten, die in einer Ebene zu zwei festen Foki oder Punkten vorhanden sind.
Alle Parabolas haben die gleiche Form, egal welche Größe; Alle Hyperbel haben unterschiedliche Formen
Die Parabola wird durch die Gleichung y2 = x gegeben; Eine Hyperbel wird durch die Gleichung xy = 1 gegeben
In einer Parabola werden die beiden Arme parallel zueinander, während sie in einer Hyperbola nicht tun.