Unterschied zwischen gegenseitig ausschließlichen und unabhängigen Ereignissen
- 4171
- 531
- Rahel Diedrich
 Die Wahrscheinlichkeit ist ein mathematisches Konzept, das jetzt zu einer vollwertigen Disziplin geworden ist und ein wesentlicher Bestandteil der Statistik ist. Zufälliges Experiment in Wahrscheinlichkeit ist eine Leistung, die ein bestimmtes Ergebnis erzeugt. Die Ergebnisse eines zufälligen Experiments werden als Ereignis bezeichnet. Wahrscheinlich gibt es verschiedene Arten von Ereignissen, wie in einfacher, zusammengesetzter, gegenseitig ausschließlicher, erschöpfender, unabhängiger, abhängiger, ebenso wahrscheinlicher Wahrscheinlichkeit usw. Wenn Ereignisse nicht gleichzeitig auftreten können, werden sie aufgerufen gegenseitig ausschließend
Die Wahrscheinlichkeit ist ein mathematisches Konzept, das jetzt zu einer vollwertigen Disziplin geworden ist und ein wesentlicher Bestandteil der Statistik ist. Zufälliges Experiment in Wahrscheinlichkeit ist eine Leistung, die ein bestimmtes Ergebnis erzeugt. Die Ergebnisse eines zufälligen Experiments werden als Ereignis bezeichnet. Wahrscheinlich gibt es verschiedene Arten von Ereignissen, wie in einfacher, zusammengesetzter, gegenseitig ausschließlicher, erschöpfender, unabhängiger, abhängiger, ebenso wahrscheinlicher Wahrscheinlichkeit usw. Wenn Ereignisse nicht gleichzeitig auftreten können, werden sie aufgerufen gegenseitig ausschließend
Andererseits werden jedes Ereignis von anderen Ereignissen nicht betroffen Unabhängige Ereignisse. Lesen Sie den unten dargestellten Artikel vollständig, um den Unterschied zwischen gegenseitig ausschließlichen und unabhängigen Ereignissen besser zu verstehen.
Inhalt: gegenseitig exklusives Ereignis gegen unabhängiges Ereignis
- Vergleichstabelle
- Definition
- Schlüsselunterschiede
- Abschluss
Vergleichstabelle
| Vergleichsgrundlage | Gegenseitig ausschließende Ereignisse | Unabhängige Ereignisse |
|---|---|---|
| Bedeutung | Zwei Ereignisse sollen sich gegenseitig ausschließen, wenn ihr Auftreten nicht gleichzeitig ist. | Zwei Ereignisse sollen unabhängig sein, wenn das Auftreten eines Ereignisses das Auftreten eines anderen nicht kontrollieren kann. |
| Beeinflussen | Das Auftreten eines Ereignisses führt zum Nicht-Auftreten des anderen. | Das Auftreten eines Ereignisses hat keinen Einfluss auf das Auftreten des anderen. |
| Mathematische Formel | P (a und b) = 0 | P (a und b) = p (a) p (b) |
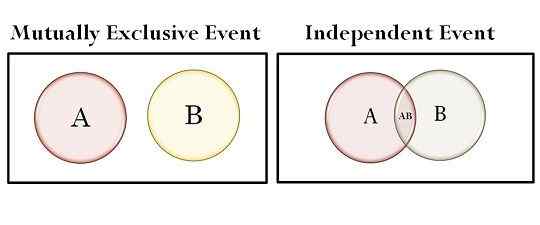
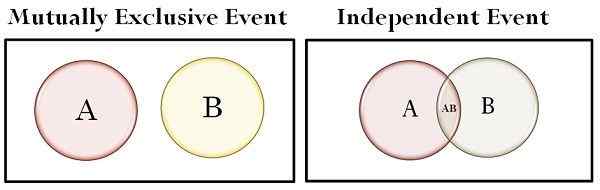
| Setzt im Venn -Diagramm ein | Überlappt sich nicht | Überlappungen |
Definition eines gegenseitig ausschließlichen Ereignisses
Gegenseitig ausschließende Ereignisse sind solche, die nicht gleichzeitig auftreten können, ich.e. Wo das Auftreten eines Ereignisses zu einem Nicht-Auftreten des anderen Ereignisses führt. Solche Ereignisse können nicht gleichzeitig wahr sein. Daher macht das Geschehen eines Ereignisses das Geschehen eines anderen Ereignisses unmöglich. Diese werden auch als disjunkte Ereignisse bezeichnet.
Nehmen wir ein Beispiel für das Werfen einer Münze, wo das Ergebnis entweder Kopf oder Schwanz wäre. Sowohl Kopf als auch Schwanz können nicht gleichzeitig auftreten. Nehmen Sie ein weiteres Beispiel an, nehmen Sie an, ob ein Unternehmen Maschinen kaufen möchte, für die es zwei Optionen Maschine A und B hat. Die kostengünstige Maschine und Produktivität ist besser, wird ausgewählt. Die Akzeptanz von Maschine A wird automatisch zur Ablehnung von Maschine B und umgekehrt führt.
Definition des unabhängigen Ereignisses
Wie der Name schon sagt, sind unabhängige Ereignisse die Ereignisse, bei denen die Wahrscheinlichkeit eines Ereignisses die Wahrscheinlichkeit des Auftretens des anderen Ereignisses nicht kontrolliert. Das Ereignis oder die Nichtverhütung eines solchen Ereignisses hat absolut keinen Einfluss auf das Ereignis oder die Nichtverhütung eines anderen Ereignisses. Das Produkt ihrer getrennten Wahrscheinlichkeiten entspricht der Wahrscheinlichkeit, dass beide Ereignisse auftreten werden.
Nehmen wir ein Beispiel, nehmen wir an, wenn eine Münze zweimal geworfen wird, Schwanz in der ersten Chance und Schwanz in der zweiten, sind die Ereignisse unabhängig. Ein weiteres Beispiel dafür: Angenommen, wenn ein Würfel zweimal, 5 im ersten Chance und 2 im zweiten, sind die Ereignisse unabhängig.
Schlüsselunterschied zwischen gegenseitig ausschließlichen und unabhängigen Ereignissen
Die signifikanten Unterschiede zwischen gegenseitig ausschließlichen und unabhängigen Ereignissen werden wie unter:
- Gegenseitig ausschließende Ereignisse sind diese Ereignisse, wenn ihr Ereignis nicht gleichzeitig ist. Wenn das Auftreten eines Ereignisses das Auftreten eines anderen nicht kontrollieren kann, werden solche Ereignisse als unabhängiges Ereignis bezeichnet.
- Bei gegenseitig ausschließlichen Ereignissen führt das Auftreten eines Ereignisses zum Nicht-Auftreten des anderen. Umgekehrt wird bei unabhängigen Ereignissen ein Ereignis keinen Einfluss auf das Auftreten des anderen haben.
- Gegenseitig ausschließende Ereignisse werden mathematisch als p (a und b) = 0 dargestellt, während unabhängige Ereignisse als P (A und B) = P (A) P (B) dargestellt werden.
- In einem Venn -Diagramm überlappen sich die Sätze nicht gegenseitig, wenn wir gegenseitig ausschließende Ereignisse haben, während wir uns überlappen, wenn wir über unabhängige Ereignisse sprechen.
Abschluss
Mit der obigen Diskussion ist es also ziemlich klar, dass beide Ereignisse nicht gleich sind. Darüber hinaus gibt es einen Punkt zu erinnern, und wenn sich ein Ereignis gegenseitig ausschließt, kann es nicht unabhängig sein und umgekehrt. Wenn sich zwei Ereignisse A und B gegenseitig ausschließen, können sie als P (AuB) = P (A)+P (B) ausgedrückt werden, während sie als P (A∩b) = ausdrücklich ausgedrückt werden können, wenn dieselben Variablen unabhängig sind P (a) p (b).
- « Unterschied zwischen Typ A und Typ B -Persönlichkeit
- Unterschied zwischen Kompensation und Leistungen »

