Unterschied zwischen Mittelwert und Median

- 2510
- 132
- Tina Gürbig
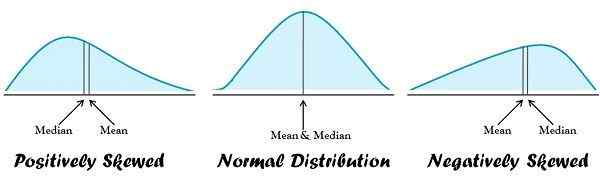 Die zentrale Tendenz impliziert die Tendenz der Datenpunkte, sich um den zentralen oder mittlersten Wert zu gruppieren. Die beiden am häufigsten verwendeten Messungen der zentralen Tendenz sind mittlere und Mediane. Bedeuten ist definiert als der "zentrale" Wert des angegebenen Datensatzes, während Median ist der mittelstenster Wert in der angegebenen Datenmenge.
Die zentrale Tendenz impliziert die Tendenz der Datenpunkte, sich um den zentralen oder mittlersten Wert zu gruppieren. Die beiden am häufigsten verwendeten Messungen der zentralen Tendenz sind mittlere und Mediane. Bedeuten ist definiert als der "zentrale" Wert des angegebenen Datensatzes, während Median ist der mittelstenster Wert in der angegebenen Datenmenge.
Ein ideales Maß für die zentrale Tendenz ist eine klar definierte, leicht verständliche, einfach kalkulierbare. Es sollte auf allen Beobachtungen beruhen und am wenigsten von extremen Beobachtungen beeinflusst werden, die im Datensatz vorhanden sind.
Menschen kontrastieren diese beiden Maßnahmen oft, aber Tatsache ist, dass sie unterschiedlich sind. Dieser Artikel unterstreicht ausdrücklich die grundlegenden Unterschiede zwischen Mittelwert und Median. Guck mal.
Inhalt: Mean gegen Median
- Vergleichstabelle
- Definition
- Schlüsselunterschiede
- Beispiel
- Abschluss
Vergleichstabelle
| Vergleichsgrundlage | Bedeuten | Median |
|---|---|---|
| Bedeutung | Der Mittelwert bezieht sich auf den einfachen Durchschnitt der angegebenen Werte oder Mengen. | Der Median ist definiert als die mittlere Zahl in einer geordneten Liste von Werten. |
| Was ist es? | Es ist ein arithmetischer Durchschnitt. | Es ist Positionsdurchschnitt. |
| Repräsentiert | Schwerpunkt des Datensatzes | Schwerpunkt des Datensatzes Mitte des Datensatzes |
| Anwendbarkeit | Normalverteilung | Verzerrte Verteilung |
| Ausreißer | Der Mittelwert ist empfindlich gegenüber Ausreißern. | Der Median ist nicht empfindlich gegenüber Ausreißern. |
| Berechnung | Der Mittelwert wird berechnet, indem alle Beobachtungen addieren und dann den Wert teilen, der mit der Anzahl der Beobachtungen erhalten wurde. | Um den Median zu berechnen, ist der Datensatz in aufsteigender oder absteigender Reihenfolge angeordnet. Der Wert, der in der genauen Mitte des neuen Datensatzes fällt, ist der Median. |
Definition von Mean
Der Mittelwert ist das weit verbreitete Maß für die zentrale Tendenz, die als Durchschnitt des Wertesatzes definiert ist. Es repräsentiert das Modell und den häufigsten Wert des angegebenen Wertebereichs. Es kann sowohl in diskreten als auch in kontinuierlichen Serien berechnet werden.
Der Mittelwert entspricht der Summe aller Beobachtungen geteilt durch die Anzahl der Beobachtungen im Datensatz. Wenn der von einer Variablen angenommene Wert gleich ist, ist sein Mittelwert auch gleich. Der Mittelwert kann zwei Arten sein, der Probenmittelwert (x̅) und der Populationsmittelwert (µ). Es kann mit gegebener Formel berechnet werden:
- Arithmetisches Mittel:
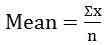 Wo ʃ = griechischer Buchstabe Sigma, bezeichnet "Summe von ..."
Wo ʃ = griechischer Buchstabe Sigma, bezeichnet "Summe von ..."
n = Anzahl der Werte - Für diskrete Serien:
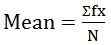 wo, f = Frequenz
wo, f = Frequenz - Für kontinuierliche Portionen:
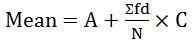 wobei d = (x-a)/c
wobei d = (x-a)/c
A = angenommen Mittelwert
C = Gemeinsamer Divisor
Definition von Median
Der Median ist ein weiteres wichtiges Maß für die zentrale Tendenz, die zum Aufteilungswert in zwei gleiche Teile verwendet wird, i.e. größere Hälfte der Stichprobe, Population oder Wahrscheinlichkeitsverteilung aus der unteren Hälfte. Es ist der mittlerste Wert, der erreicht wird, wenn die Beobachtungen in einer bestimmten Reihenfolge sortiert werden, entweder aufsteigend oder absteigender Reihenfolge.
Für die Berechnung des Medianes ordnen Sie zunächst die Beobachtungen in den niedrigsten bis höchsten oder am niedrigsten bis niedrigsten an und wenden Sie dann die entsprechende Formel an, gemäß den folgenden Bedingungen:
- Wenn die Anzahl der Beobachtungen ungerade ist:
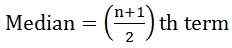 wo n = Anzahl der Beobachtungen
wo n = Anzahl der Beobachtungen - Wenn die Anzahl der Beobachtungen Ist selbst:
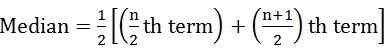
- Für kontinuierliche Serien:
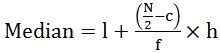 wo, l = Untergrenze der mittleren Klasse
wo, l = Untergrenze der mittleren Klasse
C = kumulative Häufigkeit der vorhergehenden Medianklasse
F = Häufigkeit der mittleren Klasse
H = Klassenbreite
Schlüsselunterschiede zwischen Mittelwert und Median
Die signifikanten Unterschiede zwischen dem Mittelwert und dem Median sind in dem nachstehenden Artikel angegeben:
- In Statistiken ist ein Mittelwert als einfacher Durchschnitt des angegebenen Satzes oder Größensatzes. Der Median soll die mittlere Zahl in einer geordneten Liste von Werten sein.
- Während der Mittelwert der arithmetische Durchschnitt ist, ist der Median der Positionsdurchschnitt. Im Wesentlichen bestimmt die Position des Datensatzes den Wert des Medianes.
- Mittelwerte beschreibt den Schwerpunkt des Datensatzes, während der Median den mittlersten Wert des Datensatzes hervorhebt.
- Der Mittelwert ist für normal verteilte Daten geeignet. Am anderen Ende ist der Median am besten, wenn die Datenverteilung verzerrt ist.
- Der Mittelwert ist stark von dem extremen Wert beeinflusst, der in dem Fall nicht bei einem Median ist.
- Der Mittelwert wird berechnet, indem alle Beobachtungen addieren und dann den Wert dividieren, der mit der Anzahl der Beobachtungen erhalten wurde; Das Ergebnis ist Mittelwert. Im Gegensatz zum Median ist der Datensatz in aufsteigender oder absteigender Reihenfolge angeordnet, und der Wert, der in der genauen Mitte des neuen Datensatzes fällt.
Beispiel
Finden Sie den Mittelwert und den Median des angegebenen Datensatzes:
58, 26, 65, 34, 78, 44, 96
Lösung: Um den Mittelwert zu berechnen, müssen Sie die Summe der Beobachtungen durch die Anzahl der Beobachtungen teilen,
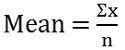
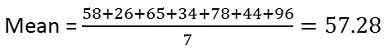 Mittelwert = 57.28
Mittelwert = 57.28
Um den Median zu berechnen, ordnen Sie die Serie in einer Sequenz an, ich.e. Niedrigste bis höchste,
26, 34, 44, 58, 65, 78, 96
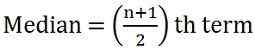 wo n = Anzahl der Beobachtungen
wo n = Anzahl der Beobachtungen
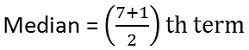 Median = 4th Begriff = 58
Median = 4th Begriff = 58
Abschluss
Nach der Überprüfung der oben genannten Punkte können wir sagen, dass diese beiden mathematischen Konzepte unterschiedlich sind. Arithmetischer Mittelwert oder Mittelwert wird als das beste Maß für die zentrale Tendenz angesehen, da er alle Merkmale eines idealen Maßes enthält, aber einen Nachteil hat, dass die Stichprobenschwankungen den Mittelwert beeinflussen.
Auf die gleiche Weise ist der Median auch eindeutig definiert und leicht zu verstehen und zu berechnen, und das Beste an dieser Maßnahme ist, dass er nicht durch Stichprobenschwankungen beeinflusst wird, aber der einzige Nachteil des Median ist, dass er nicht auf allen basiert Beobachtungen. Für die Klassifizierung der offenen Endung wird der Median normalerweise gegenüber dem Mittelwert bevorzugt.

