Unterschied zwischen Binomial- und Poisson -Verteilung

- 2275
- 223
- Caitlin Rodehau
 Der binomiale Verteilung ist einer, dessen mögliche Anzahl von Ergebnissen zwei sind, ich.e. Erfolg oder Misserfolg. Andererseits gibt es keine Grenze für mögliche Ergebnisse in Poisson-Verteilung
Der binomiale Verteilung ist einer, dessen mögliche Anzahl von Ergebnissen zwei sind, ich.e. Erfolg oder Misserfolg. Andererseits gibt es keine Grenze für mögliche Ergebnisse in Poisson-Verteilung
Die theoretische Wahrscheinlichkeitsverteilung ist definiert als eine Funktion, die den möglichen Ergebnissen des statistischen Experiments eine Wahrscheinlichkeit zuweist. Die Wahrscheinlichkeitsverteilung kann diskret oder kontinuierlich sein, wobei in der diskreten Zufallsvariablen die Gesamtwahrscheinlichkeit unterschiedlichen Massenpunkte zugeordnet wird, während in der kontinuierlichen Zufallsvariable die Wahrscheinlichkeit in verschiedenen Klassenintervallen verteilt wird.
Binomialverteilung und Poisson -Verteilung sind zwei diskrete Wahrscheinlichkeitsverteilung. Normalverteilung, Studentenverteilung, Chi-Quadrat-Verteilung und F-Verteilung sind die Arten der kontinuierlichen Zufallsvariablen. Hier gehen wir hier, um den Unterschied zwischen Binomial- und Poisson -Verteilung zu diskutieren. Guck mal.
Inhalt: Binomialverteilung gegen Poisson -Verteilung
- Vergleichstabelle
- Definition
- Schlüsselunterschiede
- Abschluss
Vergleichstabelle
| Vergleichsgrundlage | Binomiale Verteilung | Poisson-Verteilung |
|---|---|---|
| Bedeutung | Die binomiale Verteilung ist eine, bei der die Wahrscheinlichkeit einer wiederholten Anzahl von Versuchen untersucht wird. | Die Poisson -Verteilung gibt an, dass unabhängige Ereignisse mit einem bestimmten Zeitraum zufällig auftreten. |
| Natur | Biparametrisch | Uniparametrisch |
| Anzahl von Versuchen | Fest | Unendlich |
| Erfolg | Ständige Wahrscheinlichkeit | Infinitesimale Erfolgschance |
| Ergebnisse | Nur zwei mögliche Ergebnisse, ich.e. Erfolg oder Misserfolg. | Unbegrenzte Anzahl möglicher Ergebnisse. |
| Mittelwert und Varianz | Mittelwert> Varianz | Mittelwert = Varianz |
| Beispiel | Münzentwurfsexperiment. | Druckfehler/Seite eines großen Buches. |
Definition der Binomialverteilung
Binomialverteilung ist die weit verbreitete Wahrscheinlichkeitsverteilung, die aus dem Bernoulli -Prozess abgeleitet ist (ein zufälliges Experiment, das nach einem renommierten Mathematiker Bernoulli benannt ist). Es ist auch als biparametrische Verteilung bekannt, wie es durch zwei Parameter n und p vorgestellt wird. Hier ist N die wiederholten Versuche und P ist die Erfolgswahrscheinlichkeit. Wenn der Wert dieser beiden Parameter bekannt ist, bedeutet dies, dass die Verteilung vollständig bekannt ist. Der Mittelwert und die Varianz der Binomialverteilung werden durch µ = np und σ2 = npq bezeichnet.
P (x = x) = NCX PX QN-X, x = 0,1,2,3… n
= 0, sonst
Ein Versuch, ein bestimmtes Ergebnis zu erzielen, das überhaupt nicht sicher und unmöglich ist, wird als Versuch bezeichnet. Die Versuche sind unabhängig und eine feste positive Ganzzahl. Es hängt mit zwei gegenseitig ausschließlichen und erschöpfenden Ereignissen zusammen; Wenn das Auftreten als Erfolg bezeichnet wird und das Auftreten nicht auftreten wird, wird als Versagen bezeichnet. P repräsentiert die Erfolgswahrscheinlichkeit, während q = 1 - p die Wahrscheinlichkeit eines Versagens darstellt, der sich während des gesamten Prozesses nicht ändert.
Definition der Poisson -Verteilung
In den späten 1830er Jahren stellte ein berühmter französischer Mathematiker Simon Denis Poisson diese Verteilung vor. Es beschreibt die Wahrscheinlichkeit der bestimmten Anzahl von Ereignissen in einem festen Zeitintervall. Es ist eine uniparametrische Verteilung, da es nur durch einen Parameter λ oder m vorgestellt wird. In der Poisson -Verteilung wird Mittelwert mit M i bezeichnet.e. µ = m oder λ und die Varianz ist als σ gekennzeichnet2 = m oder λ. Die Wahrscheinlichkeitsmassenfunktion von x wird dargestellt durch:
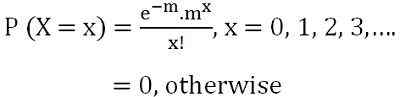 wo e = transzendentale Menge, deren ungefährer Wert 2 ist.71828
wo e = transzendentale Menge, deren ungefährer Wert 2 ist.71828
Wenn die Anzahl des Ereignisses hoch ist, die Wahrscheinlichkeit seines Auftretens ziemlich gering ist, wird die Poisson -Verteilung angewendet. Zum Beispiel die Anzahl der Versicherungsansprüche/einen Tag bei einer Versicherungsgesellschaft.
Schlüsselunterschiede zwischen Binomial- und Poisson -Verteilung
Die Unterschiede zwischen Binomial- und Poisson -Verteilung können aus den folgenden Gründen deutlich gezogen werden:
- Die Binomialverteilung ist eine, bei der die Wahrscheinlichkeit einer wiederholten Anzahl von Versuchen untersucht wird. Eine Wahrscheinlichkeitsverteilung, die die Anzahl einer Reihe unabhängiger Ereignisse in einem bestimmten Zeitraum zufällig erfolgt, wird als Wahrscheinlichkeitsverteilung bezeichnet.
- Binomiale Verteilung ist biparametrisch, ich.e. Es wird von zwei Parametern n und p vorgestellt, während die Poisson -Verteilung uniparametrisch ist, i.e. gekennzeichnet durch einen einzelnen Parameter m.
- Es gibt eine feste Anzahl von Versuchen in der Binomialverteilung. Andererseits gibt es eine unbegrenzte Anzahl von Versuchen in einer Poisson -Verteilung.
- Die Erfolgswahrscheinlichkeit ist in der Binomialverteilung konstant, aber in der Poisson -Verteilung gibt es eine äußerst geringe Anzahl von Erfolgschancen.
- In einer binomialen Verteilung gibt es nur zwei mögliche Ergebnisse, ich.e. Erfolg oder Misserfolg. Umgekehrt gibt es eine unbegrenzte Anzahl möglicher Ergebnisse bei Poisson -Verteilung.
- In der binomialen Verteilung Mittelwert> Varianz während des Poisson -Verteilungsmittelwerts = Varianz.
Abschluss
Abgesehen von den oben genannten Unterschieden gibt es eine Reihe ähnlicher Aspekte zwischen diesen beiden Verteilungen i i.e. Beide sind die diskrete theoretische Wahrscheinlichkeitsverteilung. Darüber hinaus können beide auf der Grundlage der Parameterwerte unimodal oder bimodal sein. Darüber hinaus kann die Binomialverteilung durch die Poisson -Verteilung angenähert werden.
- « Unterschied zwischen Statistik und Parameter
- Differenz zwischen dem Pooling von Interessenmethode und der Kaufmethode »

