Unterschied zwischen Bereich und Umfang
- 2673
- 474
- Prof. Dr. Charleen Lammert
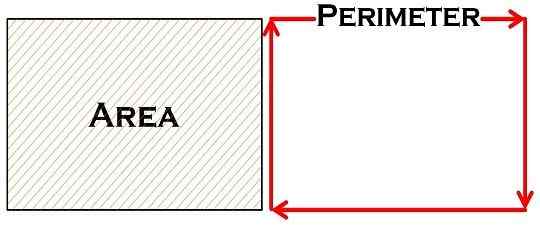
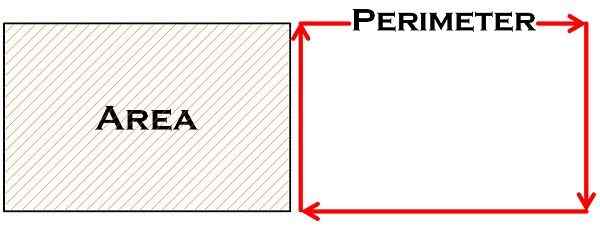Bereich und Umfang sind zwei wichtige grundlegende Konzepte der Mathematik, die oft zusammen verstanden werden. Diese beiden Konzepte werden verwendet, um den physischen Raum eines Objekts zu messen und bildet eine Grundlage für fortschrittliche Mathematik. Der Umfang wird oft als die Länge des Pfades verstanden, der eine geschlossene Figur abdeckt, während sich der Bereich auf den von der geschlossenen Figur abgedeckten Raum bezieht.
Beide Konzepte haben praktische Anwendung und werden in unserem täglichen Leben verwendet. Während der Bereich nichts anderes als das Ausmaß der Oberfläche ist, ist der Umfang die kontinuierliche Linie, die eine Grenze einer geschlossenen geometrischen Form bildet. Lesen Sie den Artikel aus, um die grundlegenden Unterschiede zwischen Bereich und Umfang zu kennen.
Inhalt: Bereich vs Perimeter
- Vergleichstabelle
- Definition
- Schlüsselunterschiede
- Formeln
- Abschluss
Vergleichstabelle
| Vergleichsgrundlage | Bereich | Umfang |
|---|---|---|
| Bedeutung | Fläche wird als Messung der Oberfläche des Objekts beschrieben. | Umfang bezieht sich auf den Umriss, der eine geschlossene Figur umgibt. |
| Repräsentiert | Raum, der von der Figur besetzt ist. | Rand oder Grenze einer Figur. |
| Messung | Quadratische Einheiten | Lineare Einheiten |
| Dimensionen beteiligt | Zwei | Eins |
| Beispiel | Platz vom Garten bedeckt. | Länge des Zauns erforderlich, um den Garten einzuschließen. |
Definition des Gebiets
In der Mathematik wird der Bereich einer flachen Oberfläche als die von ihm abgedeckte Fläche definiert. Es ist eine physikalische Menge, die die Anzahl der quadratischen Einheiten anzeigt, die vom zweidimensionalen Objekt besetzt sind. Es wird verwendet, um zu wissen, wie viel Platz von einer ebenen Fläche genommen wird. Es wird in quadratischen Einheiten gemessen, ich.e. Quadratmeter, Quadratmeilen, Quadratzoll usw.
Der Begriff Gebiet hat eine Ende der praktischen Nutzung wie bei Bauprojekten, Landwirtschaft, Architektur usw. Um den Bereich einer flachen Oberfläche zu messen, müssen Sie die Anzahl der von der Form bedeckten Quadrate zählen.
Zum Beispiel: Angenommen, Sie müssen den Boden des Raums fliesen, die Anzahl der zum Abdecken des gesamten Raums erforderlichen Kacheln ist sein Bereich.
Definition von Umfang
Der Umkreis ist definiert als ein Maß für die Länge der Grenze, die eine geschlossene geometrische Figur umgibt. Der Begriff "Perimeter" stammt aus dem griechischen Wort "Peri" und "Meter", was bedeutet und messen. In der Geometrie impliziert dies die kontinuierliche Linie, die den Weg außerhalb der zweidimensionalen Form bildet.
In einfachen Worten ist der Umfang nichts als die Länge des Umrisss einer Figur. Um den Umfang eines bestimmten Objekts herauszufinden, können Sie einfach die Länge der Seiten hinzufügen, um zu seinem Umfang zu gelangen. Der Umfang eines Kreises ist allgemein als seinen Umfang bekannt.
Zum Beispiel: A. Angenommen, Sie wickeln eine Schnur um das Quadrat, die Länge der Schnur wäre ihr Umfang.
B. Sie gehen außerhalb des Gartens herum, die abgedeckte Entfernung wäre Gartenumfang.
Schlüsselunterschiede zwischen Bereich und Umfang
Die signifikanten Unterschiede zwischen Fläche und Umfang sind in den folgenden Punkten im Detail vorgesehen:
- Die Fläche wird als Messung der Oberfläche des Objekts beschrieben. Umfang bezieht sich auf den Umriss, der eine geschlossene Figur umgibt.
- .Bereich repräsentiert den Raum, der vom Objekt besetzt ist. Umgekehrt gibt der Umfang die äußere Kante oder Grenze der Form an.
- Die Messung der Fläche erfolgt in quadratischen Einheiten I.e. Quadratkilometer, Quadratfuß, Quadratzoll usw. Andererseits wird der Umfang einer Form in linearen Einheiten i gemessen.e. Kilometer, Zoll, Füße usw.
- Da der Umkreis in linearen Einheiten gemessen wird, misst er nur eine Dimension I.e. Länge des Objekts. Während im Bereich des Gebiets zwei Dimensionen beteiligt sind, i.e. Länge und Breite des Objekts.
Formeln
| Objekt | Bereich | Umfang | Variable |
|---|---|---|---|
| Quadrat | a^2 | 4a | wo, a = Länge der Seite |
| Rechteck | L × b | 2 (l+b) | wo, l = Länge B = Breite |
| Kreis | πr^2 | 2πr = πd | wo, r = radius |
| Dreieck | 1/2 bh | a+b+c | wo, b = Basis H = Höhe A, B, C = Länge der Seiten |
| Rhombus | (pq)/2 | 4a | wo, a = Seite P und Q sind Diagonale |
| Parallelogramm | BH | 2 (a+b) | wobei B = Basis H = Höhe a = Seite |
| Trapez | ½ (a+b) × h | A+B+C+D | wobei a = Basis B = Basis H = Höhe C = Seite d = Seite |
Abschluss
Nach der Überprüfung der oben genannten Punkte ist klar, dass diese beiden mathematischen Konzepte unterschiedlich sind, aber Sie können einen verwenden, um einen anderen herauszufinden. Während der Bereich einfach bedeutet, der „Raum bedeckt“ i.e. Innerhalb des Objekts bezieht sich der Umfang auf die Distanz, ich.e. Der Umriss der Form. Darüber hinaus können Zahlen mit demselben Umfang unterschiedliche Fläche haben und Zahlen mit demselben Bereich können einen anderen Umfang haben.