Unterschiede zwischen Korrelation und Regression

Sowohl Korrelation als auch Regression sind statistische Instrumente, die sich mit zwei oder mehr Variablen befassen. Obwohl sich beide auf dieselbe Gegenstand beziehen, gibt es Unterschiede zwischen den beiden. Die Unterschiede zwischen den beiden werden nachstehend erklärt.

Bedeutung

Der Begriff Korrelation unter Bezugnahme auf zwei oder mehr Variablen bedeutet, dass die Variablen in irgendeiner Weise verwandt sind. Die Korrelationsanalyse bestimmt, ob eine Beziehung zwischen zwei Variablen existiert, und die Stärke der Beziehung. Wenn zwei Variablen x (unabhängig) und y (abhängig) so verwandt sind, dass die Variation der Größe der unabhängigen Variablen durch Variation der Größe der abhängigen Variablen begleitet wird, sollen die beiden Variablen korreliert sind.

Korrelation kann linear oder nicht linear sein. Eine lineare Korrelation ist eine, bei der die Variablen so verwandt sind, dass eine Änderung des Wertes einer Variablen zu einer Änderung des Wertes anderer Variable konsequent führt. In einer linearen Korrelation würden sich die mit den jeweiligen Werten abhängigen und unabhängigen Variablen bezogenen Punkte um eine nicht horizontale gerade Linie zusammenziehen die Variablen.

Die Regressionsanalyse hingegen verwendet die vorhandenen Daten, um eine mathematische Beziehung zwischen den Variablen zu bestimmen, die verwendet werden kann, um den Wert der abhängigen Variablen in Bezug auf jeden Wert der unabhängigen Variablen zu bestimmen.

Statistische Ausrichtung

Die Korrelation befasst sich mit der Messung der Assoziationsstärke oder der Beziehungsintensität, wobei die Regression mit der Vorhersage des Wertes der abhängigen Variablen in Bezug auf einen bekannten Wert der unabhängigen Variablen vorhersagt wird. Dies kann mit den folgenden Formeln erklärt werden.

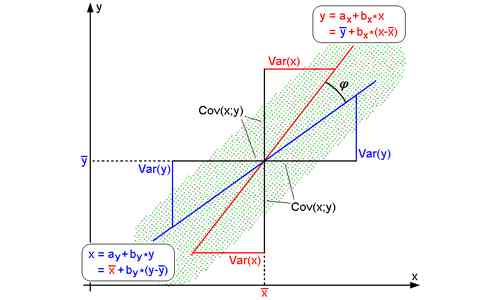
Korrelationskoeffizient oder Koeffizientkorrelation (R) zwischen X & y wird mit der folgenden Formel herausgefunden;

r = Kovarianz (x, y)/σx.σy, Cov (x, y) = σxy/n - (σx/n) (σy/n), σx & σy sind Standardabweichungen von x bzw. y, und, -1 < r 0, then correlation coefficient between x and y = correlation coefficient between u and v.

Korrelationskoeffizient R ist eine reine Anzahl und unabhängig von der Messeinheit. Wenn x also Höhe ist (Zoll) und y Gewicht (lbs.) von Menschen einer bestimmten Region ist R weder in Zoll noch in LBs., aber einfach eine Nummer.

Die Regressionsgleichung wird mit der folgenden Formel herausgefunden;

Regressionsgleichung von y auf x (um die Schätzung von y herauszufinden) ist y - y '= byx (x -x‾), BYX wird als Regressionskoeffizient von y auf x bezeichnet. Regressionsgleichung von x auf y (um die Schätzung von x herauszufinden) ist x - x '= bxy (y -y‾), BXY wird als Regressionskoeffizient von x auf y bezeichnet.

Die Korrelationsanalyse geht nicht davon aus. Es schätzt einfach den Assoziationsgrad zwischen Variablen. Mit anderen Worten, Korrelationsanalyse testet die gegenseitige Abhängigkeit von Variablen. Die Regressionsanalyse hingegen beschreibt die Abhängigkeit der abhängigen Variablen oder der Antwortvariablen von der unabhängigen oder erklärenden Variablen/s. Die Regressionsanalyse geht davon aus. Für die Korrelation sind beide Werte abhängiger und unabhängiger Variablen zufällig, aber für Regressionswerte unabhängiger Variablen müssen nicht zufällig sein.

Zusammenfassung

1. Korrelationsanalyse ist ein Test der Abhängigkeit zwischen zwei Variablen. Die Regressionsanalyse gibt eine mathematische Formel an, um den Wert der abhängigen Variablen in Bezug auf einen Wert der unabhängigen Variablen/s zu bestimmen.

2. Der Korrelationskoeffizient ist unabhängig von der Wahl von Herkunft und Skala, aber der Regressionskoeffizient ist nicht so.

Für die Korrelation müssen die Werte beider Variablen zufällig sein, aber dies ist nicht für den Regressionskoeffizienten der Fall.

Literaturverzeichnis

1. Das, n. G., (1998), Statistische Methoden, Kalkutta

2. Korrelation und Regression, erhältlich unter www erhältlich.Le.AC.brit/bl/gat/virtualfc/statistics/Regression

3. Regression und Korrelation, erhältlich unter www erhältlich.Abgrund.Uoregon.Edu