Unterschied zwischen Stichprobenvarianz und Populationsvarianz

Erläuterung

In Statistiken bezieht sich der Begriff Stichproben auf die Auswahl eines Teils der aggregierten statistischen Daten, um relevante Informationen über das Ganze zu erhalten. Das Aggregat oder die gesamte statistische Informationen zu einem bestimmten Charakter aller von der Untersuchung erfassten Mitglieder werden als "Bevölkerung" oder "Universum" bezeichnet. (Das, n.G., 2010). Der ausgewählte Teil der Bevölkerung, der verwendet wird, um die Merkmale der Bevölkerung oder des Universums zu erhalten, wird als "Stichprobe" bezeichnet. Die Bevölkerung soll aus einzelnen Einheiten oder Mitgliedern bestehen, und einige der Einheiten sind in der Stichprobe enthalten. Die Gesamtzahl der Einheiten der Bevölkerung wird als Bevölkerungsgröße bezeichnet und die der Stichprobe als Stichprobengröße bezeichnet. Bevölkerung und Stichprobe können endlich oder unendlich sein und in ähnlicher Weise können sie existieren oder hypothetisch sein.

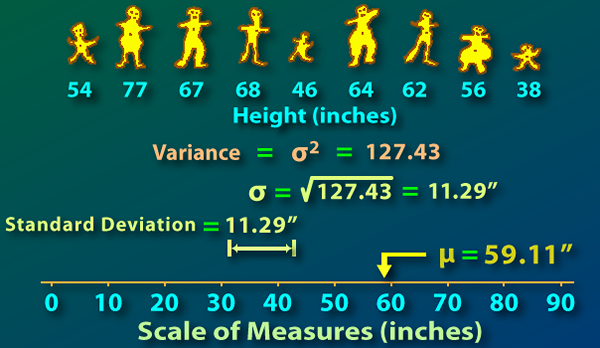
Varianz: Varianz ist ein numerischer Wert, der zeigt, wie weit die einzelnen Zahlen in einer Reihe von Daten über den Mittelwert verteilt werden. So weit ist jede Zahl vom Mittelwert und damit voneinander. Eine Varianz von Nullwert bedeutet, dass alle Daten identisch sind. Mehr die Varianz, mehr sind die Werte, die sich um den Mittelwert ausbreiten, daher voneinander. Weniger die Varianz, weniger sind die Werte, die sich um den Mittelwert ausbreiten, daher voneinander, und die Varianz kann nicht negativ sein.

Unterschied zwischen Populationsvarianz und Stichprobenvarianz

Der Hauptunterschied zwischen Populationsvarianz und Stichprobenvarianz bezieht sich auf die Berechnung der Varianz. Die Varianz wird in fünf Schritten berechnet. Der erste Mittelwert wird berechnet, dann berechnen wir Abweichungen vom Mittelwert, und drittens sind die Abweichungen quadratisch, viertens werden die quadratischen Abweichungen zusammengefasst und schließlich wird diese Summe durch Anzahl der Elemente geteilt, für die die Varianz berechnet wird. Somit Varianz = σ (xi-x-)/n. Wo xi = ith. Nummer, x- = Mittelwert und n = Anzahl der Elemente…

Wenn nun die Varianz aus Populationsdaten berechnet werden soll, entspricht n der Anzahl der Elemente. Wenn also die Varianz des Blutdrucks aller 1000 Personen aus Daten zum Blutdruck aller 1000 Personen berechnet werden soll, dann n = 1000. Wenn jedoch die Varianz aus den Probendaten berechnet wird, soll 1 von n abgezogen werden, bevor die Summe der quadratischen Abweichungen geteilt wird. Somit wäre im obigen Beispiel, wenn Beispieldaten 100 Elemente haben, der Nenner 100 - 1 = 99.

Aus diesem Grund ist der aus Stichprobendaten berechnete Varianzwert höher als der Wert, der durch Verwendung von Populationsdaten hätte herausgefunden werden können. Die Logik, dies zu tun, besteht darin, unseren Mangel an Informationen über die Bevölkerungsdaten zu kompensieren. Es ist unmöglich, die Abweichung der Höhen bei Menschen herauszufinden, für unseren absoluten Mangel an Informationen über Höhen aller lebenden Menschen, nicht um über die Zukunft zu sprechen. Auch wenn wir ein moderates Beispiel nehmen, wie Bevölkerungsdaten in Höhen aller lebenden Männer in uns, ist es physisch möglich, aber die damit verbundenen Kosten und Zeit würden den Zweck seiner Berechnung besiegen. Dies ist der Grund, warum Beispieldaten für die meisten statistischen Zwecke entnommen werden, und dies wird von mangelnden Informationen über die Mehrheit der Daten begleitet. Um dies zu kompensieren, ist der Varianzwert und die Standardabweichung, was quadratische Varianzwurzel ist.

Dies fungiert als automatischer Schild für die Analysten und Entscheidungsträger. Die Logik gilt für Entscheidungen über Kapitalbudgetierung, persönliche und geschäftliche Finanzierung, Bau, Verkehrsmanagement und viele anwendbare Bereiche. Dies hilft dem Stakeholder, sich bei der Entscheidung oder für andere Schlussfolgerungen auf der sicheren Seite zu stellen.

Zusammenfassung: Die Populationsvarianz bezieht sich auf den Varianzwert, der aus Populationsdaten berechnet wird, und die Stichprobenvarianz ist die aus Stichprobendaten berechnete Varianz. Aufgrund dieses Wertes des Nenners in der Formel für die Varianz bei Stichprobendaten ist 'N-1' und für Bevölkerungsdaten 'N'. Infolgedessen sind sowohl die Varianz als auch die Standardabweichung, die aus Stichprobendaten abgeleitet werden.