Unterschied zwischen realen Zahlen und Ganzzahlen

Mathematiker haben Systeme entwickelt, um anzugeben, wie sich eine bestimmte Zahl von einer anderen unterscheidet. Genau wie bei anderen Konzepten überschneiden sich die Nummerkategorien. Da reale Zahlen alle rationalen Zahlen wie die Ganzzahlen enthalten, teilen sie ähnliche Eigenschaften wie die Verwendung ganzer Zahlen und werden in der Zahlenlinie aufgezeichnet. Der Hauptunterschied besteht daher darin, dass reelle Zahlen eine allgemeine Klassifizierung sind, während Ganzzahlen eine Untergruppe sind, die als ganze Zahlen charakterisiert ist, die negative Eigenschaften haben können.

Was sind echte Zahlen?

Reelle Zahlen sind die Werte, die Sie in der Zahlenlinie finden, die normalerweise als geometrische horizontale Linie ausgedrückt wird, in der ein ausgewählter Punkt als „Ursprung“ fungiert. Diejenigen, die auf der rechten Seite fallen. Die Beschreibung „Real“ wurde von Rene Descartes präsentiert, einem berühmten Mathematiker und Philosoph im 17. Jahrhundert. Er hat den Unterschied zwischen den realen Wurzeln der Polynome und ihren imaginären Wurzeln besonders festgelegt.

Die realen Zahlen umfassen ganze, ganze Zahlen, natürliche, rationale und irrationale Zahlen:

• Ganze Zahlen

Ganze Zahlen sind positive Zahlen, die weder fraktionelle Teile noch Dezimalpunkte haben, da sie ganze Objekte ohne Fragmente oder Teile darstellen.

• Ganzzahlen

Ganzzahlen sind ganze Zahlen, die die negative Seite der Zahlenlinie enthalten.

• Natürliche Zahlen

Auch als Zählzahlen bezeichnet, sind natürliche Zahlen wie ganze Zahlen, aber Null ist nicht enthalten, da nichts im Wesentlichen als „0“ gezählt werden kann.

• Rationale Zahlen

In Bezug auf seine Ursprünge verkündete Pythagoras, der alte griechische Mathematiker, dass alle Zahlen rational seien. Rationale Zahlen sind die Quotienten oder die Fraktionen von zwei Ganzzahlen.  Wobei P und Q beide Ganzzahlen sind und Q nicht zu Null entspricht, ist P/Q eine rationale Zahl. Zum Beispiel ist 3/5 eine rationale Zahl, aber 3/0 nicht.

• Irrationale Zahlen

Der Student von Pythagoras, Hippasus, war anderer Meinung, dass alle Zahlen rational waren. Durch die Geometrie bewies er, dass einige Zahlen irrational waren. Zum Beispiel die Quadratwurzel von zwei, die 1 ist.41 kann nicht als Bruchteil ausgedrückt werden; Daher ist es irrational. Leider wurde die Aktualität rationaler Zahlen von den Anhängern von Pythagoras nicht akzeptiert. Dies führte dazu, dass Hippasus auf See ertrunken wurde, was in dieser Zeit eine Bestrafung der Götter war.

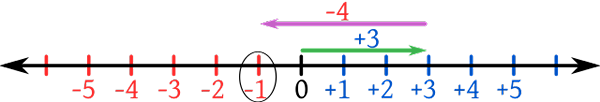
Was sind ganze Zahlen??

Aus dem lateinischen Wort "Integer", das "Ganzes" oder "unberührt" übersetzt. Die Zahlen umfassen positive natürliche Zahlen oder die Zählzahlen und deren Negative. Zum Beispiel -3, -2, -1, 0, -1, 2, 3 sind Ganzzahlen. Die übliche Abbildung sind gleichermaßen beabstandete Zahlen auf einer unendlichen Zahlenlinie mit Null, was in der Mitte weder positiv noch negativ ist. Daher sind die Positiven größer als die Negative.

In Bezug auf seine Geschichte verfolgen die folgenden Konten, wie Gauner zum ersten Mal verwendet wurden:

• In 200 b.C. Negative Zahlen wurden zuerst mit roten Stäben im alten China vertreten.
• In ungefähr 630 a.D., Negative Zahlen wurden verwendet, um Schulden in Indien zu vertreten.
• Arbermouth Holst, ein deutscher Mathematiker, stellte 1563 Zahlen als System zusätzlich und Multiplikation ein. Er entwickelte das System als Reaktion auf die zunehmende Anzahl von Kaninchen und Elefanten, auf denen er experimentierte.

Im Folgenden sind die Eigenschaften von Ganzzahlen:

• Positiv

Die Zahlen auf der rechten Seite der Zahlenlinie sind positiv und repräsentieren häufig den höheren Wert ihrer negativen Gegenstücke.

• Negativ

Die Zahlen auf der linken Seite der Zahlenlinie werden häufig als der geringere Standardwert ihrer positiven Gegenstücke angesehen.

• Neutral

Die Mitte der Zahlenlinie ist die Ganzzahl, die weder positiv noch negativ ist.

• Keine Fragmente

Wie ganze Zahlen haben Ganzzahlen weder Dezimalpunkte noch Brüche.

Unterschied zwischen realen Zahlen und Ganzzahlen

Umfang der realen Zahlen und Ganzzahlen

Die realen Zahlen sind Zahlen, rationale, irrationale, natürliche und ganze Zahlen. Auf der anderen Seite befasst sich der Umfang von ganzen Zahlen hauptsächlich mit ganzen Zahlen, die negativ und positiv sind. Daher sind reelle Zahlen allgemeiner.

Brüche

Reale Zahlen können Brüche wie rationale und irrationale Zahlen umfassen. Brüche können jedoch keine Ganzzahlen sein.

Die am wenigsten gebundene Eigenschaft

Reale Zahlen haben die am wenigsten gebundene Eigenschaft, die auch als „Vollständigkeit“ bezeichnet wird. Dies bedeutet, dass ein linearer Satz realer Zahlen Teilmengen mit supremumischen Qualitäten hat.  Im Gegenteil haben Ganzzahlen nicht das am wenigsten gebundene Eigentum.

Archimedanische Eigenschaft

Die archimedische Eigenschaft, die Annahme ist, dass es eine natürliche Zahl gibt, die gleich oder größer als jede reelle Zahl ist, kann auf reelle Zahlen angewendet werden. Im Gegenteil, das archimedische Eigentum kann nicht auf Ganzzahlen angewendet werden.

Feld

Reale Zahlen sind eine Art von Feld, eine wesentliche algebraische Struktur, in der arithmetische Prozesse definiert werden. Im Gegenteil, Ganzzahlen werden nicht als Feld betrachtet.

Zählbar

Als Set sind reelle Zahlen unzähliger, während Ganzzahlen zählbar sind.

Symbole von reellen Zahlen und Ganzzahlen

Reelle Zahlen werden als „R“ symbolisiert, während eine Reihe von Ganzzahlen als „Z“ symbolisiert wird.  N. Bourbaki, eine Gruppe französischer Mathematiker in den 1930er Jahren, spezifizierte „Z“ aus dem deutschen Wort „Zahlen“, was Zahl oder ganze Zahlen bedeutet.

Wortursprung für reelle Zahlen und Ganzzahlen

Reelle Zahlen bezeichneten die wirklichen Wurzeln eines Polynome, während die Ganzzahl aus dem lateinischen Wort stammte, „ganz“, da sie weder Dezimalstellen noch Brüche enthalten.

Reelle Zahlen gegen ganze Zahlen

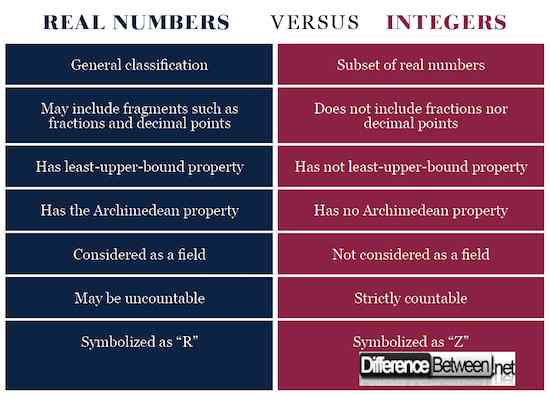
Zusammenfassung der realen Zahlen vs.  Ganzzahlen

• Sowohl reelle Zahlen als auch Ganzzahlen können auf der Zahlenlinie aufgetragen werden.
• Ganzzahlen sind eine Untergruppe realer Zahlen.
• Ganzzahlen haben negative Zahlen.
• Als Set hat reelle Zahlen im Vergleich zu Ganzzahlen einen allgemeineren Umfang.
• Im Gegensatz zu Ganzzahlen können reale Zahlen Brüche und Dezimalpunkte umfassen.
• Eigenschaften der am wenigsten gebundenen, archimedischen und Feld sind im Allgemeinen für reelle Zahlen anwendbar, aber nicht für Ganzzahlen.
• Im Gegensatz zu realen Zahlen sind Ganzzahlen streng zählbar.
• "R" steht für reelle Zahlen, während "Z" für Ganzzahlen ist.