Unterschied zwischen FFT und DFT

Fast Fourier Transform (FFT) vs. Diskrete Fourier -Transformation (DFT)

Technologie und Wissenschaft gehen Hand in Hand. Und es gibt kein besseres Beispiel dafür als digitale Signalverarbeitung (DSP). Die digitale Signalverarbeitung ist der Prozess zur Optimierung der Genauigkeit und Effizienz der digitalen Kommunikation. Alles sind Daten - sei es die Bilder aus Außenraumsonden oder seismischen Schwingungen und irgendetwas dazwischen. Um diese Daten mithilfe von Computern in das menschliche lesbare Format umzuwandeln, ist die digitale Signalverarbeitung. Es ist eine der mächtigsten Technologien, die sowohl die mathematische Theorie als auch die physikalische Implementierung kombiniert. Die Untersuchung von DSP begann als Graduiertenkurs in der Elektrotechnik, ist jedoch im Laufe der Zeit zu einem potenziellen Gamechanger im Bereich Wissenschaft und Ingenieurwesen geworden. Es genügt zu sagen, ohne DSP könnten Ingenieure und Wissenschaftler aufhören zu existieren.

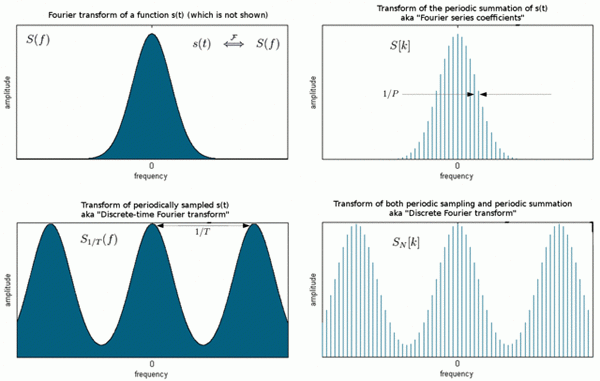
Fourier -Transformation ist ein Mittel zur Zuordnung eines Signals in der Zeit- oder Raumdomäne in sein Spektrum in der Frequenzdomäne. Die Zeit- und Frequenzdomänen sind nur alternative Möglichkeiten, Signale darzustellen, und die Fourier -Transformation ist die mathematische Beziehung zwischen den beiden Darstellungen. Eine Signaländerung in einer Domäne würde auch das Signal in der anderen Domäne beeinflussen, aber nicht unbedingt auf die gleiche Weise. Discrete Fourier -Transformation (DFT) ist eine Transformation wie Fourier -Transformation, die mit digitalisierten Signalen verwendet wird. Wie der Name schon sagt, handelt es sich um die diskrete Version des FT, die sowohl die Zeitdomäne als auch die Frequenzdomäne als periodisch betrachtet. Fast Fourier Transform (FFT) ist nur ein Algorithmus für eine schnelle und effiziente Berechnung des DFT.

Diskrete Fourier -Transformation (DFT)

Die diskrete Fourier-Transformation (DFT) ist eines der wichtigsten Tools in der digitalen Signalverarbeitung, das das Spektrum eines Finite-Dauer-Signals berechnet. Es ist sehr häufig, die Informationen in den Sinusoiden zu codieren, die ein Signal bilden. In einigen Anwendungen ist die Form einer Zeitdomänenwellenform jedoch nicht die Anwendung für Signale. In diesem Fall wird Signalfrequenzinhalt in anderen Weise als als digitale Signale sehr nützlich. Die Darstellung eines digitalen Signals in Bezug auf seine Frequenzkomponente in einem Frequenzbereich ist wichtig. Der Algorithmus, der die Zeitdomänensignale in die Frequenzdomänenkomponenten umwandelt, wird als diskrete Fourier -Transformation oder DFT bezeichnet.

Schnelle Fourier -Transformation (FFT)

Die Fast Fourier -Transformation (FFT) ist eine Implementierung des DFT, die fast die gleichen Ergebnisse wie die DFT liefert, aber unglaublich effizienter und viel schneller ist, was die Rechenzeit oft erheblich verkürzt. Es ist nur ein Computeralgorithmus, der für eine schnelle und effiziente Berechnung des DFT verwendet wird. Verschiedene schnelle DFT -Berechnungstechniken, die gemeinsam als Fast Fourier -Transformation oder FFT bezeichnet werden. Gauß war der erste, der die Technik zur Berechnung der Koeffizienten in einem trigonometrischen Asteroidenumlaufraum 1805 vorschlug. Erst 1965 erregte jedoch ein wegweisendes Papier von Cooley und Tukey die Aufmerksamkeit der Wissenschafts- und Ingenieurgemeinschaft, die auch die Grundlage für die Disziplin der digitalen Signalverarbeitung legte.

Unterschied zwischen FFT und DFT

1. Bedeutung von FFT und DFT

Diskrete Fourier -Transformation oder einfach als DFT bezeichnet, ist der Algorithmus, der die Zeitdomänensignale in die Frequenzdomänenkomponenten umwandelt. DFT ist, wie der Name schon sagt, wirklich diskret; Datensätze mit diskreten Zeitdomänen werden in diskrete Frequenzdarstellung umgewandelt. In einfachen Worten stellt es eine Beziehung zwischen der Zeitdomänendarstellung und der Frequenzdomänendarstellung her. Fast Fourier -Transformation oder FFT ist ein Computeralgorithmus, der die Rechenzeit und Komplexität großer Transformationen verkürzt. FFT ist nur ein Algorithmus, der für die schnelle Berechnung des DFT verwendet wird.

2. Algorithmus von FFT und DFT

Der am häufigsten verwendete FFT-Algorithmus ist der Cooley-Tukey-Algorithmus, der nach J benannt wurde. W. Cooley und John Tukey. Es handelt sich. Es bricht die DFT in kleinere DFTs zusammen. Weitere FFT-Algorithmen sind der Algorithmus des Strichers, Winograd Fourier-Transformationalgorithmus, Chirp Z-Transform-Algorithmus usw. Die DFT -Algorithmen können entweder auf Digitalcomputern Allzwecke programmiert oder direkt von Special Hardware implementiert werden. Der FFT -Algorithmus wird verwendet, um die DFT einer Sequenz oder ihrer Umkehrung zu berechnen. Ein DFT kann als o (n) durchgeführt werden²) In der Zeitkomplexität, während FFT die zeitliche Komplexität in der Reihenfolge von O (NLOGN) verringert.

3. Anwendungen von FFT und DFT

DFT kann in vielen digitalen Verarbeitungssystemen für eine Vielzahl von Anwendungen verwendet werden, z. FFT wurde häufig für akustische Messungen in Kirchen und Konzertsälen verwendet. Weitere Anwendungen von FFT umfassen Spektralanalysen in analogen Videomessungen, Multiplikation mit großer Ganzzahl und Polynom, Filteralgorithmen, Berechnung von Isotopenverteilungen, Berechnung von Fourier -Serienkoeffizienten, Berechnung von Konvolutionen, Erzeugen von Rauschen mit niedrigem Frequenz, Entwurf von Kinoforms, Durchführung dicht strukturierter Matrizen, Bildverarbeitung und Erzeugung von Kinoformen, Bildverarbeitung und Bearbeitung und Bearbeitung von Kinoformen, Bildverarbeitung und Bildung und Bildung und Bildung, Bildverarbeitung, Bildverarbeitung und Bearbeitung von Kinoformen mehr.

Fft vs. DFT: Vergleichstabelle

Zusammenfassung von FFT vs. DFT

Kurz gesagt spielt die diskrete Fourier -Transformation eine Schlüsselrolle in der Physik, da sie als mathematisches Instrument verwendet werden kann. Es ist ein einfacher, aber ziemlich zeitaufwändiger Algorithmus. Um die Rechenzeit und Komplexität großer Transformationen zu verkürzen, kann jedoch ein komplexerer, aber weniger zeitaufwändiger Algorithmus wie die schnelle Fourier-Transformation verwendet werden. FFT ist eine Implementierung der DFT, die für die schnelle Berechnung des DFT verwendet wird. Kurz gesagt, FFT kann alles tun, was ein DFT tut, aber effizienter und viel schneller als ein DFT. Es ist eine effiziente Art, die DFT zu berechnen.