Unterschied zwischen Differential und Derivat

Um den Unterschied zwischen Differential und Ableitung einer Funktion besser zu verstehen, müssen Sie zuerst das Konzept einer Funktion verstehen.

Eine Funktion ist eines der grundlegenden Konzepte in der Mathematik, die eine Beziehung zwischen einer Reihe von Eingängen und einer Reihe möglicher Ausgänge definieren, bei denen jeder Eingang mit einem Ausgang zusammenhängt. Eine Variable ist die unabhängige Variable und die andere Variable ist die abhängige Variable.

Das Konzept der Funktion ist eines der am meisten unterschätzten Themen in der Mathematik, ist jedoch für die Definition physischer Beziehungen von wesentlicher Bedeutung. Nehmen wir zum Beispiel: Die Anweisung „Y ist eine Funktion von x“ bedeutet, dass etwas, das mit Y zusammenhängt. Nehmen wir an, wenn die Eingabe 6 ist und die Funktion 5 zum Eingang 6 hinzufügen soll 6. Das Ergebnis beträgt 6+5 = 11, was Ihre Ausgabe ist.

Es gibt nur wenige Ausnahmen in der Mathematik oder Sie können Probleme sagen, die nicht durch gewöhnliche Methoden der Geometrie und Algebra gelöst werden können. Ein neuer Mathematikzweig, der als Kalkül bekannt ist, wird verwendet, um diese Probleme zu lösen.

Calculus unterscheidet sich grundlegend von der Mathematik, die nicht nur die Ideen aus Geometrie, Arithmetik und Algebra verwendet, sondern sich auch mit Veränderung und Bewegung befasst.

Der Kalkül als Werkzeug definiert die Ableitung einer Funktion als Grenze einer bestimmten Art. Das Konzept der Ableitung einer Funktion unterscheidet die Berechnung von anderen Zweigen der Mathematik. Das Differential ist ein Kalkül -Unterfeld, das sich auf den Infinitesimal in einer verschiedenen Menge bezieht und eine der beiden grundlegenden Abteilungen von Kalkül ist. Der andere Zweig wird als Integral Calculus bezeichnet.

Was ist Differential?

Differential ist eine der Fundamentals -Abteilungen des Kalküls zusammen mit Integral Calculus. Es handelt. Die Welt, in der wir leben, ist voller miteinander verbundener Mengen, die sich regelmäßig verändern.

Zum Beispiel der Bereich eines kreisförmigen Körpers, der sich ändert, wenn sich der Radius ändert, oder ein Projektil, das sich mit der Geschwindigkeit ändert. Diese wechselnden Einheiten werden in mathematischer Begriffen als Variablen bezeichnet und die Änderungsrate einer Variablen in Bezug auf eine andere ist ein Derivat. Und die Gleichung, die die Beziehung zwischen diesen Variablen darstellt, wird als Differentialgleichung bezeichnet.

Differentialgleichungen sind Gleichungen, die unbekannte Funktionen und einige ihrer Derivate enthalten.

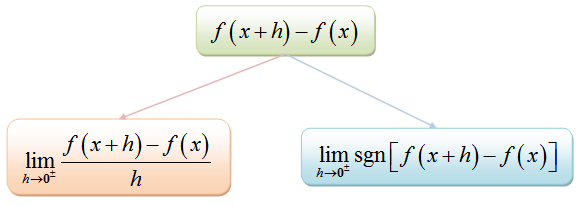
Was ist derivat?

Das Konzept der Ableitung einer Funktion ist eines der mächtigsten Konzepte in der Mathematik. Die Ableitung einer Funktion ist normalerweise eine neue Funktion, die als Ableitungsfunktion oder Ratenfunktion bezeichnet wird.

Die Ableitung einer Funktion stellt eine momentane Änderungsrate des Wertes einer abhängigen Variablen in Bezug auf die Änderung des Wertes der unabhängigen Variablen dar. Es ist ein grundlegendes Berechnungswerkzeug, das auch als Steigung der Tangentenlinie interpretiert werden kann. Es misst, wie stark der Diagramm einer Funktion an einem bestimmten Punkt im Diagramm liegt.

In einfachen Worten ist Ableitung die Rate, mit der sich die Funktion zu einem bestimmten Zeitpunkt ändert.

Unterschied zwischen Differential und Derivat

Definition von Differential vs. Derivat

Sowohl die Begriffe Differential als auch Derivat sind in Bezug auf die Wechselbeziehung eng miteinander verbunden. In der Mathematik werden wechselnde Entitäten als Variablen bezeichnet, und die Änderungsrate einer Variablen in Bezug auf eine andere wird als Ableitung bezeichnet.

Gleichungen, die die Beziehung zwischen diesen Variablen und ihren Derivaten definieren, werden als Differentialgleichungen bezeichnet. Differenzierung ist der Prozess der Suche nach einem Derivat. Die Ableitung einer Funktion ist die Änderungsrate des Ausgangswerts in Bezug auf ihren Eingangswert, während differenz die tatsächliche Änderung der Funktion ist.

Verhältnis von Differential vs. Derivat

Differenzierung ist eine Methode zum Berechnen eines Derivats, das die Änderungsrate der Ausgabe y der Funktion in Bezug auf die Änderung der Variablen x ist.

In einfachen Worten bezieht sich derivat auf die Änderungsrate von Y in Bezug auf x, und diese Beziehung wird als y = f (x) ausgedrückt, was bedeutet, dass y eine Funktion von x ist. Die Ableitung der Funktion f (x) ist definiert als die Funktion, deren Wert die Steigung von f (x) erzeugt, in der sie definiert ist, und f (x) differenzierbar ist. Es bezieht sich auf die Neigung der Grafik an einem bestimmten Punkt.

Darstellung von Differential vs. Derivat

Unterschiede werden als dargestellt als DX, Dy, Dt und so weiter, wo DX stellt eine kleine Änderung in x dar, Dy ist eine kleine Veränderung in y und Dt ist eine kleine Änderung in t. Beim Vergleich von Änderungen in verwandten Größen, bei denen y die Funktion von x ist, ist das Differential Dy kann geschrieben werden als:

Dy = f^''(X) DX

Die Ableitung einer Funktion ist die Steigung der Funktion an jedem Punkt und wird als geschrieben als D/DX. Zum Beispiel kann die Ableitung der Sünde (x) geschrieben werden als:

D/Dx sin (x) = sin (x)^'' = cos (x)

Differential vs. Derivat: Vergleichstabelle

Zusammenfassung der Differential vs. Derivat

In der Mathematik wird die Änderungsrate einer Variablen in Bezug auf eine andere Variable als Ableitung bezeichnet, und die Gleichungen, die die Beziehung zwischen diesen Variablen und ihren Derivaten ausdrücken, werden als Differentialgleichungen bezeichnet. Kurz gesagt, Differenzierungsgleichungen betreffen Derivate, die tatsächlich angeben, wie sich eine Menge in Bezug auf einen anderen ändert. Durch die Lösung einer Differentialgleichung erhalten Sie eine Formel für die Menge, die keine Derivate enthält. Die Methode zur Berechnung eines Derivats wird als Differenzierung bezeichnet. In einfachen Worten ist die Ableitung einer Funktion die Änderungsrate des Ausgangswerts in Bezug auf ihren Eingangswert, während Differenz die tatsächliche Änderung der Funktion ist.