Unterschied zwischen kommutativem und assoziativem Unterschied

Mathematik ist ein Spiel von Zahlen und Zahlen, die überall sind. Und die Regel des Spiels sind die Eigenschaften und Regeln, die mit Zahlen verbunden sind. Immobilien helfen Ihnen dabei, die Antworten in Ihrem Kopf schnell und einfach zu berechnen. Eigenschaften sind nichts als besondere Regeln, denen Zahlen folgen. Es gibt drei grundlegende Eigenschaften von Zahlen, denen jedes mathematische System folgt: kommutative, assoziative und verteilte Eigenschaften. Diese Eigenschaften sind Funktionen der vier Vorgänge (hinzufügen, subtrahieren, multiplizieren und teilen), die immer gelten, unabhängig von der Anzahl, mit der Sie arbeiten. Wir werden jedoch nur kommutative und assoziative Eigenschaften im folgenden Artikel diskutieren.

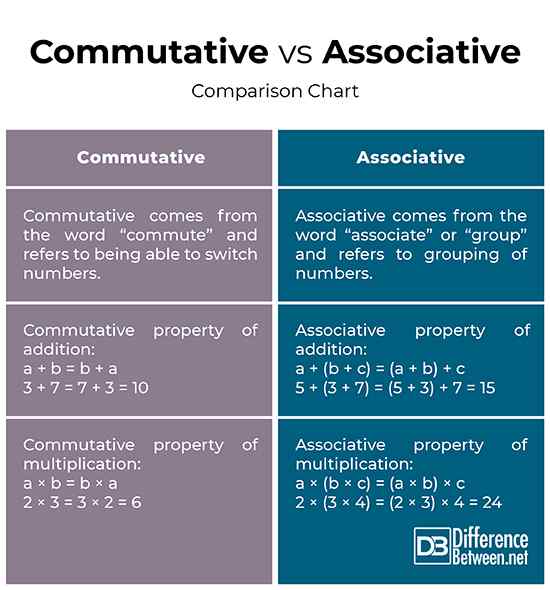
Sowohl kommutative als auch assoziative Eigenschaften sind Regeln, die für Additions- und Multiplikationsoperationen angewendet werden. Diese Eigenschaften sind Gesetze, die in Algebra verwendet werden, um Probleme zu lösen. Die kommutative Eigenschaft stammt aus dem Begriff „Pendler“, was bedeutet, sich bewegen und sich darauf bezieht, dass Sie die Nummern wechseln oder multiplizieren können. Die assoziative Eigenschaft stammt aus dem Wort „Assoziat“ oder „Gruppe“ und bezieht sich auf die Gruppierung von drei oder mehr Zahlen mit Klammern, unabhängig davon, wie Sie sie gruppieren. Das Ergebnis bleibt gleich, egal wie Sie die Zahlen neu gruppieren. Schauen wir uns die beiden Eigenschaften an, um besser zu verstehen, wie sie funktionieren.

Was ist kommutativ?

Zum Beispiel; Wir wissen, dass das Hinzufügen von 2 und 5 die gleiche Antwort wie das Hinzufügen von 5 und 2 gibt. Die Reihenfolge der Zahlen in einem Additionsproblem kann geändert werden, ohne das Ergebnis zu ändern. Dieses Ding über Zahlen und Addition wird als kommutative Eigenschaft von Addition bezeichnet. Wir können also sagen, dass Addition eine kommutative Operation ist. In ähnlicher Weise ist die Multiplikation ein kommutativer Betrieb.

Kommutative Eigenschaft der Addition:

a + b = b + a

3 + 4 = 7 ist das gleiche wie 4 + 3 = 7

Das Ergebnis wird unabhängig von der Reihenfolge der Zahlen gleich sein.

Gemeinschaftseigenschaft der Multiplikation:

a × b = b × a

3 × 7 = 21 ist das gleiche wie 7 × 3 = 21

Ebenso wird das Ergebnis unabhängig von der Reihenfolge der Zahlen gleich sein.

Was ist assoziativ?

Associativ ist eine weitere Eigenschaft, die wir verwenden. Zum Beispiel können wir beim Hinzufügen von 2 + 3 + 5 zuerst 2 und 3 hinzufügen und dann 5 hinzufügen oder zuerst 3 und 5 und dann die 2 hinzufügen. Mathematisch sieht es so aus: 2 + 3 + 5 = 2 + (3 + 5) = (2 +3) + 5. Operationen, die sich auf diese Weise verhalten, werden als assoziative Operationen bezeichnet. Das Ergebnis bleibt gleich, selbst wenn wir die Gruppierung von Zahlen ändern.

Assoziative Eigenschaft von Addition:

a + (b + c) = (a + b) + c = a + b + c

1 + (2 +3) = (1 +2) + 3 = 6

Das Ergebnis bleibt gleich, egal wie Sie die Zahlen gruppieren.

Assoziative Eigenschaft der Multiplikation:

a × (b × c) = (a × b) × c

2 × (3 × 4) = 2 × 12 = 24

(2 × 3) × 4 = 6 × 4 = 24

Die Gruppierung in den Zahlen ändert das Ergebnis nicht.

Unterschied zwischen kommutativem und assoziativem Unterschied

Bedeutung

- Die kommutative Eigenschaft stammt aus dem Begriff „Pendelverkehr“, was bedeutet, dass sie sich bewegen und sich darauf beziehen, dass Sie die Zahlen hinzufügen oder multiplizieren können, die Sie hinzufügen oder multiplizieren können. Die assoziative Eigenschaft hingegen stammt aus dem Wort „Associate“ oder „Group“ und bezieht sich auf die Gruppierung von drei oder mehr Zahlen mit Klammern, unabhängig davon, wie Sie sie gruppieren. Das Ergebnis ist das gleiche, egal wie Sie die Zahlen oder Variablen neu gruppieren.

Regel

- Die kommutative Regel der Additionszustände A + B = B + A, was bedeutet, A und B hinzuzufügen, ergibt dasselbe Ergebnis wie das Hinzufügen von B und A. Die Bestellungen können Änderungen sein, ohne das Ergebnis zu ändern. Diese Additionsregel wird als kommutative Eigenschaft von Addition bezeichnet. In ähnlicher Weise ist die Multiplikation eine kommutative Operation, was bedeutet, dass A × B das gleiche Ergebnis wie B × A ergibt. Das assoziative Eigentum hingegen ist die Regel, die sich auf die Gruppierung von Zahlen bezieht. Die assoziative Regel der Additionszustände ist das gleiche wie (a + b) + c. Ebenso sagt die assoziative Regel der Multiplikation, dass a × (b × c) das gleiche ist wie (a × b) × c.

Beispiel

- Die kommutative Eigenschaft der Zugabe: 1 + 2 = 2 +1 = 3

Die kommutative Eigenschaft der Multiplikation: 2 × 3 = 3 × 2 = 6

Die assoziative Eigenschaft von Addition: 5 + (3 + 7) = (5 + 3) + 7 = 15

Die assoziative Eigenschaft der Multiplikation: 5 × (2 × 4) = (5 × 2) × 4 = 40

Kommutativ vs. Assoziativ: Vergleichstabelle

Zusammenfassung

Kurz gesagt, das kommutative Eigentum soll nicht mit dem assoziativen Eigentum verwechselt werden. Die kommutative Eigenschaft besagt, dass es in Ordnung ist, die Reihenfolge der Zahlen zusätzlich und Multiplikationsvorgänge zu ändern, da das Ergebnis gleich sein wird, unabhängig von der Reihenfolge. Die assoziative Eigenschaft hingegen gibt an, dass das Ergebnis das gleiche sein wird, unabhängig davon, wie Sie die Anzahl oder Variablen zusätzlich/Multiplikationsoperationen gruppieren.