Unterschied zwischen Codomäne und Bereich

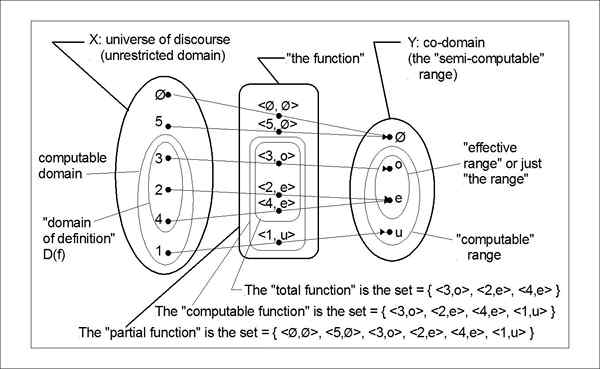
Sowohl Codomäne als auch Reichweite sind die Vorstellungen von Funktionen, die in der Mathematik verwendet werden. Während beide mit der Ausgabe zusammenhängen, ist der Unterschied zwischen beiden ziemlich subtil. Der Begriff „Bereich“ wird manchmal verwendet, um sich auf "Codomain" zu beziehen.  Wenn Sie zwischen den beiden unterscheiden, können Sie die Codomäne als Ausgabe bezeichnen, die die Funktion zur Erzeugung deklariert wird. Der Begriffsbereich ist jedoch mehrdeutig, da er manchmal genau so verwendet werden kann, wie Codomain verwendet wird. Lass uns nehmen F: A -> b, wo F ist die Funktion von a bis b. Dann ist B die Codomäne der Funktion “FUnd Bereich ist der Satz von Werten, die die Funktion übernimmt, die von bezeichnet wird F (A). Bereich kann gleich oder weniger als Codomäne sein, kann aber nicht größer sein als das.

Sei a = 1, 2, 3, 4, 5 und b = 1, 4, 8, 16, 25, 64, 125. Die Funktion F: A -> b wird durch definiert von F (x) = x ^3. Also hier,

Domain = Setzen Sie a

Codomain = set b und

Bereich (r) = 1, 8, 64, 125

Der Bereich sollte Würfel von Set A sein, aber der Würfel von 3 (dh 27) ist im Satz B nicht vorhanden. Der Bereich ist die Teilmenge der Codomäne.

Was ist Codomäne einer Funktion?

Die „Codomäne“ einer Funktion oder Beziehung ist eine Reihe von Werten, die möglicherweise daraus herauskommen könnten. Es ist tatsächlich Teil der Definition der Funktion, aber es schränkt die Ausgabe der Funktion ein. Nehmen wir zum Beispiel die Funktionsnotation F: R -> r. Es bedeutet das F ist eine Funktion von den realen Zahlen zu den realen Zahlen. Hier ist Codomain der Satz realer Zahlen R oder der Satz möglicher Ausgänge, die daraus entstehen. Domain ist auch die Menge der reellen Zahlen r. Hier können Sie auch die Funktion oder Beziehung angeben, um alle negativen Werte einzuschränken, die die Ausgabe erzeugt. In einfachen Worten ist die Codomäne ein Satz, in dem die Werte einer Funktion fallen.

Sei n der Satz natürlicher Zahlen und die Beziehung ist definiert als r = (x, y): y = 2x, x, y ∈ N

Hier sind X und Y immer natürliche Zahlen. So,

Domain = n und

Codomain = n Das ist der Satz natürlicher Zahlen.

Was ist Bereich einer Funktion??

Der „Bereich“ einer Funktion wird als die Reihe von Werten bezeichnet, die sie erzeugt oder einfach als Ausgangssatz ihrer Werte. Der Begriffsbereich wird häufig als Codomäne verwendet, aber im breiteren Sinne ist der Begriff für die Teilmenge der Codomäne reserviert. In einfachen Worten ist der Bereich der Satz aller Ausgangswerte einer Funktion und Funktion die Korrespondenz zwischen der Domäne und dem Bereich. In der nativen Set -Theorie bezieht sich der Bereich auf das Bild der Funktion oder der Codomäne der Funktion. In der modernen Mathematik wird häufig verwendet, um sich auf das Bild einer Funktion zu beziehen. Ältere Bücher beziehen sich auf das, was derzeit als Codomain und moderne Bücher bekannt ist, im Allgemeinen den Begriff Reichweite, um sich auf das zu beziehen, was derzeit als Bild bekannt ist. Die meisten Bücher verwenden den Wortbereich überhaupt nicht, um Verwirrungen insgesamt zu vermeiden.

Zum Beispiel sei A = 1, 2, 3, 4 und B = 1, 4, 9, 25, 64. Die Funktion F: A -> b wird durch definiert von F (x) = x ^2. Set a ist also die Domäne und set b die Codomäne und Bereich = 1, 4, 9. Der Bereich ist das Quadrat von A wie durch die Funktion definiert, aber das 16 -jährige Quadrat ist weder im Codomäne noch im Bereich vorhanden.

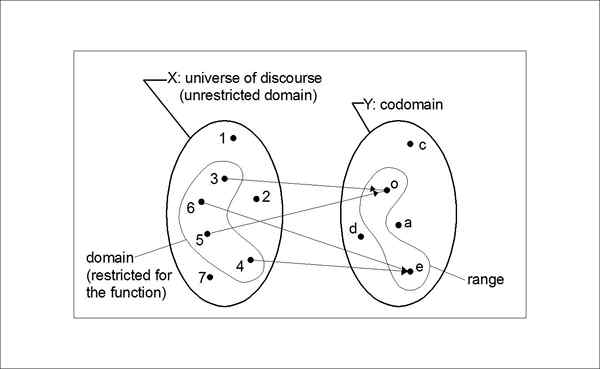
Unterschied zwischen Codomäne und Bereich

Definition von Codomäne und Reichweite

Beide Begriffe beziehen sich auf die Ausgabe einer Funktion, aber der Unterschied ist subtil. Während das Codomäne einer Funktion Werte ist, die möglicherweise daraus herauskommen, ist es tatsächlich Teil der Definition der Funktion, schränkt jedoch die Ausgabe der Funktion ein. Eine Funktionsbereich hingegen bezieht sich auf den Satz von Werten, die sie tatsächlich erzeugt.

Zweck von Codomain und Reichweite

Das Codomäne einer Funktion ist eine Reihe von Werten, die den Bereich enthält, aber einige zusätzliche Werte enthalten können. Der Zweck der Codomäne besteht darin, die Ausgabe einer Funktion einzuschränken. Der Bereich kann manchmal schwer angeben, aber ein größerer Satz von Werten, die den gesamten Bereich enthalten. Die Codomäne einer Funktion dient manchmal den gleichen Zweck wie der Bereich.

Beispiel für Codomäne und Reichweite

Wenn a = 1, 2, 3, 4 und b = 1, 2, 3, 4, 5, 6, 7, 8, 9 und die Beziehung F: A -> b wird durch definiert von F (x) = x ^2, dann codomain = set b = 1, 2, 3, 4, 5, 6, 7, 8, 9 und Bereich = 1, 4, 9. Der Bereich ist das Quadrat von Set A, aber das Quadrat von 4 (dh 16) ist weder in Set B (Codomain) noch in der Reichweite vorhanden.

Codomain vs. Bereich: Vergleichstabelle

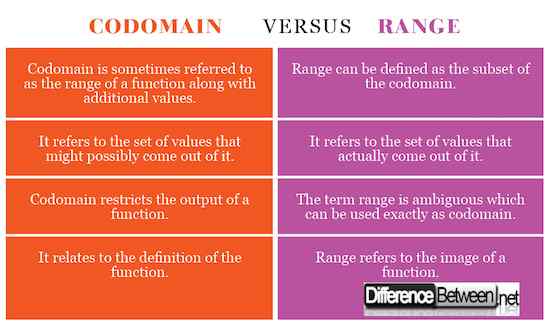
Zusammenfassung von Codomain vs. Bereich

Während beide gemeinsame Begriffe sind, die in der Theorie der nativen Menge verwendet werden, ist der Unterschied zwischen beiden ziemlich subtil. Das Codomäne einer Funktion kann einfach als Set ihrer möglichen Ausgabewerte bezeichnet werden. In mathematischer Hinsicht ist es als Ausgabe einer Funktion definiert. Der Bereich einer Funktion hingegen kann als die Reihe von Werten definiert werden, die tatsächlich daraus entstehen. Der Begriff ist jedoch mehrdeutig, was bedeutet, dass er manchmal genau wie die Codomäne verwendet werden kann. In der modernen Mathematik wird jedoch die Reichweite als Untergruppe von Codomain beschrieben, jedoch im weitaus breiteren Sinne.