Unterschied zwischen ASA und AAS

ASA vs AAS: ASA steht für "Winkel, Seite, Winkel", während AAS "Winkel, Winkel, Seite" bedeutet

Geometrie macht Spaß. Bei der Geometrie dreht sich alles um Formen, Größen und Abmessungen. Geometrie ist die Art von Mathematik, die sich mit dem Studium der Formen befasst. Es ist leicht zu erkennen, warum Geometrie so viele Anwendungen hat, die sich auf das wirkliche Leben beziehen. Es wird in allem verwendet - in Engineering, Architektur, Kunst, Sport und vielem mehr. Heute werden wir die Dreieck -Geometrie, insbesondere Dreieckkongruenz, diskutieren. Aber zuerst müssen wir verstehen, was es bedeutet, kongruent zu sein. Zwei Zahlen sind kongruent, wenn einer so auf den anderen verlegt werden kann, dass alle ihre Teile übereinstimmen. Mit anderen Worten, zwei Zahlen werden kongruent bezeichnet, wenn sie die gleiche Form und Größe haben. Zwei kongruente Zahlen sind eine und dieselbe Zahl an zwei verschiedenen Orten.

Es ist wahr als Triangle Congonce ist der grundlegende Baustein für viele geometrische Konzepte und Beweise. Dreieckkongruenz ist eines der häufigsten geometrischen Konzepte in der High School Studies. Ein wichtiges Konzept, das oft übersehen wird, wie das Lehren und Lernen über Dreieckkongruenz ist, ist das Konzept der Auslegung, dh die Bedingungen, die erfüllen, dass zwei Dreiecke kongruent sind. Es gibt fünf Möglichkeiten, um festzustellen, ob zwei Dreiecke kongruent sind, aber wir werden nur zwei diskutieren, dh ASA und AAS. ASA steht für "Winkel, Seite, Winkel", während AAS "Winkel, Winkel, Seite" bedeutet. Schauen wir uns an, wie Sie die beiden verwenden, um festzustellen, ob zwei Dreiecke kongruent sind.

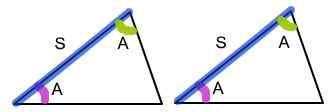
Was ist ASA -Dreieck Kongruenz?

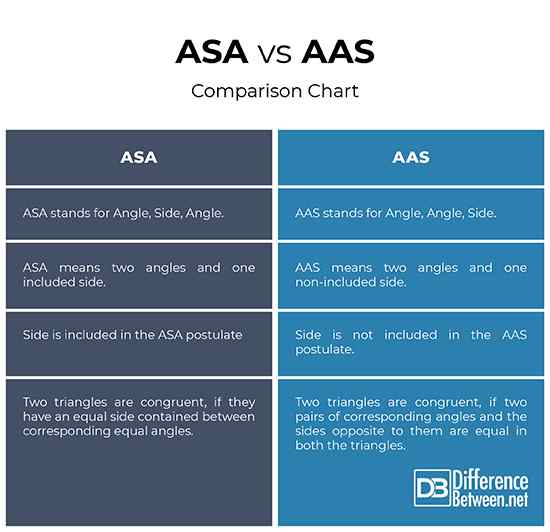
ASA steht für „Winkel, Seite, Winkel“, was bedeutet. Wenn die Eckpunkte von zwei Dreiecken in einer zu eins-Korrespondenz so sind, dass zwei Winkel und die eingeschlossene Seite eines Dreiecks kongruent zu den beiden Winkeln und der enthaltenen Seite der zweiten Dreiecke sind, dann erfüllt es den Zustand, dass die Dreiecke sind kongruent. Da die beiden Winkel und die eingeschlossene Seite in beiden Dreiecken gleich sind, werden die Dreiecke kongruent bezeichnet.

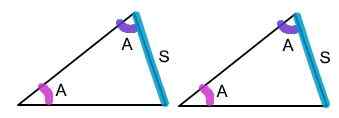
Was ist AAS -Dreieck Kongruenz?

AAS steht für „Winkel, Winkel, Seite“, was zwei Winkel und eine gegenüberliegende Seite bedeutet. AAS ist eine der fünf Möglichkeiten, um festzustellen, ob zwei Dreiecke kongruent sind. Es heißt, wenn die Eckpunkte von zwei Dreiecken in einer zu eins-Korrespondenz so sind, dass zwei Winkel und die Seite entgegengesetzt zu einem von ihnen in einem Dreieck mit den entsprechenden Winkeln und der nicht eingelegten Seite des zweiten Dreiecks übereinstimmen Die Dreiecke sind kongruent. Die Nicht-include-Seite ist die Seite gegenüber einem der beiden gewünschten Winkel. In einfachen Worten, wenn zwei Paare entsprechender Winkel und die gegenüberliegenden Seiten in beiden Dreiecken gleich sind, sind die beiden Dreiecke kongruent.

Unterschied zwischen ASA und AAS

Terminologie von ASA und AAS

- ASA und AAS sind zwei Postulate, die uns helfen, festzustellen, ob zwei Dreiecke kongruent sind. ASA steht für "Winkel, Seite, Winkel", während AAS "Winkel, Winkel, Seite" bedeutet. Zwei Zahlen sind kongruent, wenn sie die gleiche Form und Größe haben. Mit anderen Worten, zwei kongruente Zahlen sind ein und dieselbe Zahl an zwei verschiedenen Stellen. Während beide die in Beweise verwendeten Geometriebegriffe sind und sich auf die Platzierung von Winkeln und Seiten beziehen, liegt der Unterschied darin, wann sie verwendet werden sollen. ASA bezieht.

Kongruenz

- Laut ASA Kongruenz sind zwei Dreiecke kongruent, wenn sie eine gleiche Seite zwischen den entsprechenden gleichen Winkeln enthalten. Mit anderen Worten, wenn zwei Winkel und eine eingeschlossene Seite eines Dreiecks gleich den entsprechenden Winkeln und der eingeschlossenen Seite des zweiten Dreiecks sind, werden die beiden Dreiecke gemäß der ASA -Regel als kongruent bezeichnet. Die AAS-Regel hingegen gibt an, dass, wenn sich die Eckpunkte von zwei Dreiecken in eins zu eins Korrespondenz befinden, so dass zwei Winkel und die Seite entgegengesetzt zu einem von ihnen in einem Dreieck gleich den entsprechenden Winkeln und der Nicht-Winkeln sind enthalten die Seite des zweiten Dreiecks, dann sind die Dreiecke kongruent.

Darstellung

- Der Hauptunterschied zwischen den beiden Kongruenzregeln besteht darin, dass die Seite im ASA -Postulat enthalten ist, während die Seite nicht in das AAS -Postulat einbezogen wird.

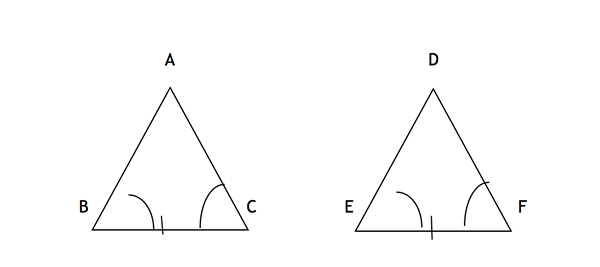
Hier stehen zwei Winkel (ABC und ACB) und die enthaltene Seite (BC) mit den entsprechenden Winkeln (DEF und DFE) und einer enthaltenen Seite (EF), wodurch die beiden Dreiecke gemäß der ASA -Kongruenzregel kongruent sind.

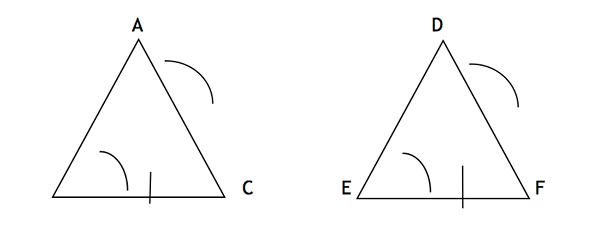
Hier stimmen zwei Winkel (ABC und BAC) und eine nicht eingelegte Seite (BC) des ersten Dreiecks mit den entsprechenden Winkeln (DEF und EDF) und der nicht eingelegten Seite (EF) des zweiten Dreiecks überein Zwei Dreiecke kongruent. AC und EF können auch die nicht eingelegten Seiten der beiden Dreiecke sein.

ASA vs. AAS: Vergleichstabelle

Zusammenfassung von ASA vs. Aas

Kurz gesagt, ASA und AAS sind zwei der fünf Congruenzregeln, die feststellen, ob zwei Dreiecke kongruent sind. ASA steht für „Winkel, Seite, Winkel“, was bedeutet. AAS bezieht sich auf „Winkel, Winkel, Seite“, was bedeutet, dass die beiden Dreiecke kongruent bezeichnet werden. Während beide im Grunde dasselbe sind, besteht der Hauptunterschied zwischen den beiden Kongruenzregeln darin, dass die Seite in der ASA -Regel enthalten ist, während die Seite nicht in der AAS -Regel enthalten ist.